 B .
B . 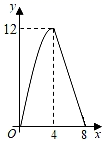 C .
C . 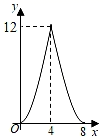 D .
D . 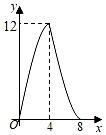
|
x |
… |
-3 |
-2 |
-1 |
| | | | 1 | 2 | 3 | … |
| y | … | … |
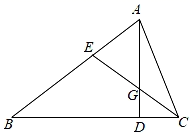
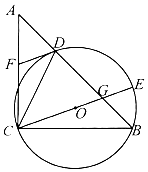
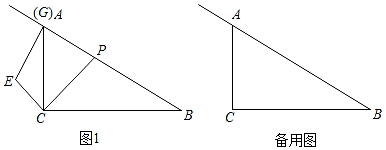
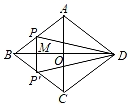
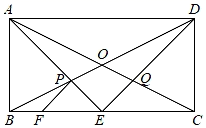
①求 的值;
②当AE=AP=2时,求PC的长;
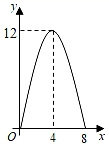
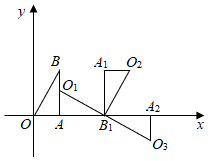
①若线段O'B'与抛物线有一个公共点,结合函数图象,请直接写出n的取值范围;
②直线PB'交抛物线于M、N两点,若点B'是线段MN的中点,求n的值.