内蒙古自治区乌海市海勃湾区2020-2021学年九年级上学期...

更新时间：2021-11-29 浏览次数：79 类型：期末考试

一、单选题

1. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020七上·太康期中) 2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为（）

A . 0.215×10⁸ B . 2.15×10⁷ C . 2.15×10⁶ D . 21.5×10⁶

答案解析收藏纠错 + 选题
3. (2020九上·海勃湾期末) 下列运算正确的是（）

A . （﹣2a³）²＝4a⁶ B . a²•a³＝a⁶ C . 3a+a²＝3a³ D . （a﹣b）²＝a²﹣b²

答案解析收藏纠错 + 选题
4. (2020九上·海勃湾期末) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数为4， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数为6，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数为（）

A . 5 B . 4.8 C . 5.2 D . 8

答案解析收藏纠错 + 选题
5. (2020·河北) 如图1，已知 $\text{[math]}$ ，用尺规作它的角平分线．
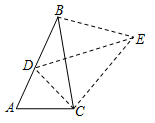
如图2，步骤如下，

第一步：以B为圆心，以a为半径画弧，分别交射线 BA ， BC 于点D，E；

第二步：分别以D，E为圆心，以b为半径画弧，两弧在 $\text{[math]}$ 内部交于点P；

第三步：画射线 BP ．射线 BP 即为所求．

下列正确的是（）

A . a，b均无限制 B . $\text{[math]}$ ， $\text{[math]}$ 的长 C . a有最小限制，b无限制 D . $\text{[math]}$ ， $\text{[math]}$ 的长

答案解析收藏纠错 + 选题
6. (2016·娄底) “数学是将科学现象升华到科学本质认识的重要工具”，比如在化学中，甲烷的化学式CH₄ ，乙烷的化学式是C₂H₆ ，丙烷的化学式是C₃H₈ ， …，设碳原子的数目为n（n为正整数），则它们的化学式都可以用下列哪个式子来表示（　　）

A . C_nH_2n+2 B . C_nH_2n C . C_nH_2n_﹣₂ D . C_nH_n+3

答案解析收藏纠错 + 选题
7. (2019九上·汕头期末) 如图，正八边形ABCDEFGH中，∠EAG大小为（）

A . 30° B . 40° C . 45° D . 50°

答案解析收藏纠错 + 选题
8. (2020九上·翁牛特旗期末) 如图，ABCD的对角线AC、BD相交于点O，EF、GH过点O，且点E、H在边AB上，点G、F在边CD上，向▱ABCD内部投掷飞镖（每次均落在▱ABCD内，且落在▱ABCD内任何一点的机会均等）恰好落在阴影区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019·北京) 用三个不等式 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
10. (2020九上·海勃湾期末) 设a，b是方程x²+x-2009=0的两个实数根，则a²+2a+b的值为（　　）

A . 2006 B . 2007 C . 2008 D . 2009

答案解析收藏纠错 + 选题
11. (2020九上·海勃湾期末) 如图，将△ABC绕点C顺时针旋转得到△DEC ，使点A的对应点D恰好落在边AB上，点B的对应点为E ，连接BE ，下列四个结论：
①AC＝AD；②AB⊥EB；③BC＝EC；④∠A＝∠EBC；

其中一定正确的是（）

A . ①② B . ②③ C . ③④ D . ②③④

答案解析收藏纠错 + 选题
12. (2020九上·海勃湾期末) 如图所示，已知二次函数y＝ax²+bx+c的图象与x轴交于A ， B两点，与y轴交于点C ， OA＝OC ，对称轴为直线x＝1，则下列结论：①abc＜0；②a+ $\text{[math]}$ b+ $\text{[math]}$ c＞0；③ac+b+1＝0；④2+c是关于x的一元二次方程ax²+bx+c＝0的一个根．其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

13. 如图，若 $\text{[math]}$ ，则表示 $\text{[math]}$ 的值的点落在（填序号）

答案解析收藏纠错 + 选题
14. (2020·郑州模拟) 不等式组 $\text{[math]}$ 的最小整数解是.

答案解析收藏纠错 + 选题
15. (2020九上·海勃湾期末) 代数式2a²-b=7，则10-4a²+2b的值是

答案解析收藏纠错 + 选题
16. 已知：如图是由若干个大小相同的小正方体所搭成的几何体从正面、左面和上面看到的形状图，则搭成这个几何体的小正方体的个数是．

答案解析收藏纠错 + 选题
17. 如图，在菱形ABCD中，对角线AC，BD交于点O，∠ABC=60°，AB=2，分别以点A、点C为圆心，以AO的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．（结果保留 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
18. 如图所示的网格是正方形网格，则 $\text{[math]}$ ＝°（点A，B，P是网格线交点）.

答案解析收藏纠错 + 选题
19. 如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为 $\text{[math]}$ 上的动点，点M，N，P分别是AD，DC，CB的中点．若⊙O的半径为4，则PN+MN的长度的最大值是．

答案解析收藏纠错 + 选题
20. 在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．
对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是．

答案解析收藏纠错 + 选题

三、解答题

21. 为了全面建设“资源节约型、环境友好型”两型社会，我国正全力推进垃圾分类工作．垃圾分类通过分类投放、分类收集，把有用物资从垃圾中分离出来重新回收、利用，变废为宝．既提高垃圾资源利用水平，又可减少垃圾处置量．它是实现垃圾减量化和资源化的重要途径和手段．为了促进学生的垃圾分类的意识与行动，市教育局决定开展“垃圾分类知识竞赛”活动．某校团委为了落实此次活动，组织全校5000名学生进行了“垃圾分类知识竞赛”初赛活动，并随机抽取了部分初赛同学的成绩，整理并绘制成如图两个图表（部分末完成）．请你根据表中提供的信息，解答问题．

分数段	频数	频率
60≤x＜70	30	0.1
70≤x＜80	90	n
80≤x＜90	m	0.4
90≤x＜100	60	0.2

（1）此次调查的样本容量为；m＝；n＝；
（2）补全频数分布直方图；
（3）已知全校共有四名同学均取得100分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校团委将从这四名同学中随机选出两名参加市级比赛，请用列举法或树状图法求甲、乙两名同学都被选中的概率．

答案解析收藏纠错 + 选题

22. (2020九上·海勃湾期末) 交通安全是社会关注的热点问题，安全隐患主要是超速和超载．某中学八年级数学活动小组的同学进行了测试汽车速度的实验．如图，先在笔直的公路1旁选取一点P，在公路1上确定点O、B，使得PO⊥l，PO＝100米，∠PBO＝45°．这时，一辆轿车在公路1上由B向A匀速驶来，测得此车从B处行驶到A处所用的时间为3秒，并测得∠APO＝60°．此路段限速每小时80千米，试判断此车是否超速？请说明理由（参考数据： $\text{[math]}$ ＝1.41， $\text{[math]}$ ＝1.73）．

答案解析收藏纠错 + 选题
23. (2020九上·海勃湾期末) 为迎接国庆节，某商店购进了一批成本为每件30元的纪念商品．经调查发现，该商品每天的销售量 $\text{[math]}$ （件 $\text{[math]}$ 与销售单价 $\text{[math]}$ （元 $\text{[math]}$ 满足一次函数关系，其图象如图所示．
1. （1）求该商品每天的销售量y与销售单价x的函数关系式；
2. （2）若商店按不低于成本价，且不高于60元的单价销售，则销售单价定为多少，才能使销售该商品每天获得的利润 $\text{[math]}$ （元 $\text{[math]}$ 最大？最大利润是多少？
答案解析收藏纠错 + 选题
24. (2020九上·海勃湾期末) 如图，在⊙O中，点D为AB的中点，点P为半径OC延长线上一点，连结AC ， AP ，且AC平分∠PAB ．
1. （1）求证：PA是⊙O的切线；
2. （2）若AB平分OC ，且⊙O的半径为2，求PA的长度．
答案解析收藏纠错 + 选题
25. (2020九上·房县期中) 如图1，E是正方形ABCD中CD边上的一点，以点A为中心，把 $\text{[math]}$ 顺时针旋转α后，得到 $\text{[math]}$ .
1. （1）求α的值；
2. （2）当点F在BC上，且∠EAF=45°，连接EF（如图2），求证：BF+DE=EF；
3. （3）在（2）的前提下，连接BD，分别交AE，AF于M，N两点（如图3），试判断线段BN，MN，DM三者的关系式，请给出证明.
答案解析收藏纠错 + 选题
26. (2018·资阳) 已知：如图，抛物线y=ax²+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．
1. （1）求抛物线的解析式；
2. （2）当点P运动到什么位置时，△PAB的面积有最大值？
3. （3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题