陕西省宝鸡市陈仓区2021-2022学年九年级上学期数学期中...

更新时间：2021-12-23 浏览次数：64 类型：期中考试

一、单选题

1. (2021九上·陈仓期中) 下列方程是一元二次方程的是（）

A . 2x﹣3y+1 B . 3x+y＝z C . x²﹣5x＝1 D . x²﹣ $\text{[math]}$ +2＝0

答案解析收藏纠错 + 选题
2. (2021九上·陈仓期中) 如图，将矩形ABCD沿对角线BD折叠，使点C落在F处，BF交AD于点E．若∠BDC＝62°，则∠DEF的度数为（）

A . 31° B . 28° C . 62° D . 56°

答案解析收藏纠错 + 选题
3. (2021九上·陈仓期中) 若方程 $\text{[math]}$ 没有实数根，则 $\text{[math]}$ 的值可以是（）

A . -1 B . 0 C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·陈仓期中) 如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，则应添加的条件是（）

A . AB//CD B . AC⊥BD C . AC=BD D . AD=BC

答案解析收藏纠错 + 选题
5. (2021九上·陈仓期中) 某班学生做“用频率估计概率”的实验时，给出的某一结果出现如图所示的统计图，则符合这一结果的实验可能是（　　）

A . 抛一枚硬币，出现正面朝上 B . 从标有1，2，3，4，5，6的六张卡片中任抽一张，出现偶数 C . 从一个装有6个红球和3个黑球的袋子中任取一球，取到的是黑球 D . 先后两次掷一枚质地均匀的正六面体骰子，两次向上的点数之和是7

答案解析收藏纠错 + 选题
6. (2021九上·陈仓期中) 如图，在菱形ABCD中，对角线AC，BD相交于点O，BD＝6，AC＝8，直线OE⊥AB交CD于点F，则EF的长为（）

A . 4.8 B . $\text{[math]}$ C . 5 D . 6

答案解析收藏纠错 + 选题
7. (2024九上·云岩月考) 已知 $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的一个根，则m的值为（）

A . -1或2 B . -1 C . 2 D . 0

答案解析收藏纠错 + 选题
8. (2021八上·台儿庄期中) 如图，在矩形ABCD中，AB＝5，AD＝3，点E为BC上一点，把△CDE沿DE翻折，点C 恰好落在AB边上的F处，则CE的长是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2021九上·陈仓期中) 中国古代数学家杨辉的《田亩比数乘除减法》中记载：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步？翻译成数学问题是：一块矩形田地的面积为864平方步，它的宽比长少12步，问它的长与宽各多少步？利用方程思想，设宽为x步，则依题意列方程为．

答案解析收藏纠错 + 选题
10. (2024九下·长春模拟) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则实数 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
11. (2021九上·陈仓期中) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 时，四边形 $\text{[math]}$ 是菱形.

答案解析收藏纠错 + 选题
12. (2023九上·嘉祥月考) 若m是方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
13. (2021九上·陈仓期中) 如图，在边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是边 $\text{[math]}$ 、 $\text{[math]}$ 上的动点.且 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题

三、解答题

14. (2021九上·陈仓期中) 用配方法解方程 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2021九上·陈仓期中) 公式法解一元二次方程：2x²﹣4x﹣1＝0.

答案解析收藏纠错 + 选题
16. (2024九下·普陀会考) 小敏与小霞两位同学解方程 $\text{[math]}$ 的过程如下框：

小敏：

两边同除以 $\text{[math]}$ ，得

$\text{[math]}$ ，

则 $\text{[math]}$ ．

小霞：

移项，得 $\text{[math]}$ ，

提取公因式，得 $\text{[math]}$ ．

则 $\text{[math]}$ 或 $\text{[math]}$ ，

解得 $\text{[math]}$ ， $\text{[math]}$ ．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

答案解析收藏纠错 + 选题
17. (2021九上·陈仓期中) 如图，四边形ABCD为正方形，连接AC，请用尺规作图法在边BC上求作一点P，使得点P到AC的距离等于BP的长度.（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题

18. (2021九上·陈仓期中) 王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球试验，每次摸出一个球（有放回），表格是活动进行中的一组统计数据：

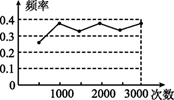
摸球的次数 $\text{[math]}$	100	150	200	500	800	1000
摸到黑球的次数 $\text{[math]}$	23	31	60	130	203	251
摸到黑球的频率 $\text{[math]}$	0.23	0.21	0.30	0.26	0.235	0.251

（1）根据上表数据估计从袋中摸出一个球是黑球的概率是；（精确到 $\text{[math]}$ ）
（2）估算袋中白球的个数.

答案解析收藏纠错 + 选题

19. (2021九上·东营月考) “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水箱亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．
1. （1）如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；
2. （2）按照（1）中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．
答案解析收藏纠错 + 选题
20. (2022九上·阳山期中)
已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．

答案解析收藏纠错 + 选题
21. (2023·乌当模拟) 为庆祝建党100周年，某大学组织志愿者周末到社区进行党史学习宣讲，决定从A ， B ， C ， D四名志愿者中通过抽签的方式确定两名志愿者参加．抽签规则：将四名志愿者的名字分别写在四张完全相同不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字，
1. （1） “A志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；
2. （2）请你用列表法或画树状图法表示出这次抽签所有可能的结果，并求出A ， B两名志愿者被选中的概率．
答案解析收藏纠错 + 选题
22. (2021·恩施模拟) 如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．
1. （1）求证：△ABF≌△ECF；
2. （2）若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．
答案解析收藏纠错 + 选题
23. (2021九上·陈仓期中) 关于x的一元二次方程x²﹣3x＋k＝0有实数根.
1. （1）求k的取值范围；
2. （2）若k是符合条件的最大整数，求此时一元二次方程的解.
答案解析收藏纠错 + 选题
24. (2021九上·陈仓期中) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 的直线分别交 $\text{[math]}$ 、 $\text{[math]}$ 边于点 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）当 $\text{[math]}$ 时，求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
25. (2023九上·同心月考) 列方程（组）解应用题
端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：

小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克．

根据他们的对话，解决下面所给问题：超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？

答案解析收藏纠错 + 选题
26. (2021九上·陈仓期中) 如图1，对角线互相垂直的四边形叫做垂美四边形.
1. （1）概念理解：如图2，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，问四边形 $\text{[math]}$ 是垂美四边形吗？请说明理由；
2. （2）性质探究：如图1，四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ .试证明： $\text{[math]}$ ；
3. （3）解决问题：如图3，分别以 $\text{[math]}$ 的直角边 $\text{[math]}$ 和斜边 $\text{[math]}$ 为边向外作正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ ，连结 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ .已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题