 B .
B .  C .
C .  D .
D . 
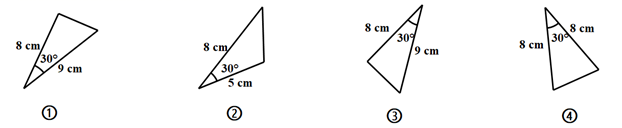







解:延长CD到H,使DH=CD,连接AH,
∵DC⊥BC,∴∠BCD=90°,( ▲ )
∵∠ACB=120°,∴∠ACD=30°,
∵D为AB的中点,∴AD=BD,( ▲ )
在△ADH与△BDC中,
∴△ADH≌△BDC(SAS),
∴AH= BC=4,( ▲ )
∠H=∠BCD=90°,( ▲ )
∵∠ACH=30°,
∴AC=8.( ▲ )

( 1 )作出△ABC关于x轴对称的图形 ,并写出点
的坐标;
( 2 )作出△ABC关于y轴对称的图形 ,并写出点
的坐标.
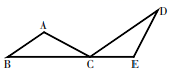

如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(选填“>”,“<”或“=”).
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出,AEDB(选填“>”,“<”或“=”);理由如下:过点E作EF∥BC,交AC于点F.(请你完成以下解答过程).
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,则CD=.