山西省晋中市祁县、灵石县2021-2022学年九年级上学期期...

更新时间：2021-12-17 浏览次数：128 类型：期中考试

一、单选题

1. (2021·厦门模拟) 如图所示的几何体的主视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021九上·灵石期中) 若一元二次方程的根为 $\text{[math]}$ ，则该一元二次方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·灵石期中) 如图：在△ABC中，点D在BC边上，连接AD，GE $\text{[math]}$ BD且交AB于点E，GF $\text{[math]}$ AC且交CD于点F，则下列结论一定正确的是（）

A . $\text{[math]}$ ＝ $\text{[math]}$ B . $\text{[math]}$ ＝ $\text{[math]}$ C . $\text{[math]}$ ＝ $\text{[math]}$ D . $\text{[math]}$ ＝ $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·大连期中) “杂交水稻之父”袁隆平和他的团队探索培育的“海水稻”在某试验田的产量逐年增加，2018年平均亩产量约500公斤，2020年平均亩产量约800公斤．若设平均亩产量的年平均增长率为x ，根据题意，可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九上·灵石期中) $\text{[math]}$ ABC~ $\text{[math]}$ ，若AB： $\text{[math]}$ =3：4，则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·灵石期中) 下列长度的各组线段中，成比例线段的是（）

A . 1cm，2cm，3cm，4cm B . 1cm，2cm，3cm，6cm C . 2cm，4cm，6cm，8cm D . 3cm，4cm，5cm，10cm

答案解析收藏纠错 + 选题
7. (2021九上·通川期中) 根据下列各组条件，不能判定△ABC∽△A₁B₁C₁的是（）

A . ∠B＝∠B₁＝60°，∠C＝50°，∠A₁＝70° B . ∠C＝∠C₁＝90°，AB＝10，AC＝6，A₁B₁＝5，A₁C₁＝3 C . ∠A＝40°，AB＝2，AC＝3，∠A₁＝40°，A₁B₁＝4，A₁C₁＝5 D . AB＝12，BC＝15，AC＝24，A₁B₁＝8，A₁C₁＝16，B₁C₁＝10

答案解析收藏纠错 + 选题
8. (2021九上·灵石期中) 方程 $\text{[math]}$ 根的情况是（）

A . 有两个不相等的实数根 B . 没有实数根 C . 有两个相等的实数根 D . 有一个实数根

答案解析收藏纠错 + 选题
9. (2021九上·灵石期中) 如图是一个游戏转盘，连续自由转动转盘两次（如果落在分隔线上，则重新转动，直至转到其中一块区域），则两次转动指针都落在数字“Ⅲ”所示区域内的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021九上·灵石期中) 如图，在△ABC中，∠ABC＝90°，AB＝8cm，BC＝6cm，动点P，Q分别从点A，B同时开始移动（移动方向如图所示），点P的速度为1cm/s，点Q的速度为2cm/s，点Q移动到C点后停止，点P也随之停止运动，当四边形APQC的面积为9cm²时，则点P运动的时间是（）

A . 3s B . 3s或5s C . 4s D . 5s

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·灵石期中) 某校篮球队进行篮球投篮训练，下表是某队员投篮的统计结果，根据上表可知该队员一次投篮命中的概率大约是．（精确到 $\text{[math]}$ ）

投篮次数/次	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
命中次数/次	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
命中率	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

答案解析收藏纠错 + 选题

12. (2021九上·灵石期中) 根据三视图，这个几何体的侧面积是．

答案解析收藏纠错 + 选题
13. (2021九上·金塔期末) 如图，在长为20m，宽为12m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为整个矩形面积的 $\text{[math]}$ ，如果设道路的宽为x m，则根据题意可列出方程．

答案解析收藏纠错 + 选题
14. (2021九上·西安期中) 如图，C、D是线段AB的两个黄金分割点，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2021九上·灵石期中) 如图，在矩形ABCD中，点N为边BC上不与B、C重合的一个动点，过点N作MN⊥BC交AD于点M，交BD于点E，以MN为对称轴折叠矩形ABNM，点A、B的对应点分别是G，F，连接EF、DF，若AB＝3，BC＝4，当△DEF为直角三角形时，CN的长为．

答案解析收藏纠错 + 选题
16. (2021九上·灵石期中) 阅读与思考
探索位似的性质

利用图形计算器或计算机等信息技术工具，可以很方便地将图形放大或缩小，还可以探索位似的性质．

小明利用几何画板软件，尝试用“观察—猜想-验证—应用”的方法进行探究，步骤如下∶如图（1），任意画一个△ABC，以点O为位似中心，自选新旧图形的相似比为k，得到△A´B´C´．

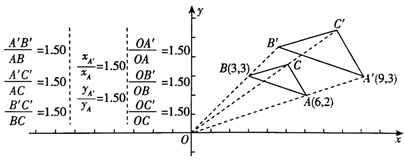
图（1）

第一步，度量对应边的长度，并计算它们的比值，发现结果与k的值相等．

第二步，以0为原点建立平面直角坐标系，分别度量点A，A´的横坐标，并计算比值；分别度量点A，A´的纵坐标，并计算比值，观察比值与k的关系，发现它们相等．接下来对其他顶点进行相同的操作，得出相同的结论．

第三步，作线段 OA，OA´，OB，OB´，OC，OC´，度量它们，发现的结论是：_________．

第四步，任意改变△ABC的位置成形状，发现上面探究得出的结论仍然成立．

于是，小明总结并得出了位似的性质．

任务∶
1. （1）第三步发现的结论是：．．
2. （2）已知图（1）中A（6，2），A´（9，3），B（3，3），S_△_ABC=2，则点B´的坐标是，S_△_A´B´C´=．
3. （3）如图（2），以点A为位似中心，画出与矩形 ABCD的相似比为0.75的一个图形．
答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·灵石期中) 用适当的方法解下列方程：
1. （1） 2x²﹣2x﹣1＝0；
2. （2） x（2x﹣5）＝4x﹣10；
答案解析收藏纠错 + 选题
18. (2021九上·灵石期中) 下面是小勇解一元二次方程的过程，请认真阅读并完成相应的任务．
解∶2x²＋4x-6=0

二次项系数化为1，得x²+2x-3=0．……………………… 第一步

移项，得x²+2x=3．…………………………………… ……第二步

配方，得x²+2x+4=3+4．即（x+2）²=7．…………… ………第三步

由此，可得x+2=± $\text{[math]}$ ． ………………………………… 第四步

x₁=2＋ $\text{[math]}$ ，x₂=2- $\text{[math]}$ ．……………………………………第五步

任务∶
1. （1）上面小勇同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元—次方程，体现的数学思想是；其中配方法依据的一个数学公式是；
2. （2） “第二步”变形的依据；
3. （3）上面小勇同学的解题过程中，从第 ▲ 步开始出现错误，写出正确的解答过程．
答案解析收藏纠错 + 选题

19. (2021九上·交城期末) “共和国勋章”获得者钟南山院士说：按照疫苗保护率达到70%计算，中国的新冠疫苗覆盖率需要达到近80%，才有可能形成群体免疫，本着自愿的原则，18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗.居民甲、乙准备接种疫苗，其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗，提供疫苗种类如下表：

接种地点		疫苗种类
医院	A	新冠病毒灭活疫苗
医院	B	重组新冠病毒疫苗（CHO细胞）
社区卫生服务中心	C	新冠病毒灭活疫苗
社区卫生服务中心	D	重组新冠病毒疫苗（CHO细胞）

若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗，且选择每个接种点的机会均等（提示：用A、B、C、D表示选取结果）

（1）求居民甲接种的是新冠病毒灭活疫苗的概率；
（2）请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率.

答案解析收藏纠错 + 选题

20. (2021九上·灵石期中) 如图，是公园的一圆形桌面的主视图，表示该桌面在路灯下的影子．
1. （1）请你在图中找出路灯的位置（要求保留画图痕迹，光线用虚线表示）；
2. （2）若桌面直径和桌面与地面的距离均为1.2m，测得影子的最大跨度为2m，求路灯O与地面的距离．
答案解析收藏纠错 + 选题
21. (2021九上·灵石期中) 抖音，是由字节跳动孵化的一款音乐创意短视频社交软件．该软件于2016年9月20日上线，是一个面向全年龄的短视频社区平台．近年来很多商家利用抖音直播平台让自己的产品大卖，某农户小王借助直播平台，计划在今年7月销售800斤奇异果，每斤奇异果定价为29元．
1. （1）经过7月试销售，小王发现每斤奇异果售价每降低0.2元，销量将增加20斤，若计划每月奇异果的销售总量为1200斤，则每斤奇异果售价应定为多少元？
2. （2）由于抖音直播的推广作用，奇异果的线下销售也终于迎来了复苏，在线上、线下销售单价一致的情况下，8月线上、线下的销售总额为30000元．受季节的影响，9月价格进行了一定调整，线下单价与（1）问中的售价保持一致，线上单价在（1）问的售价基础上提高了 $\text{[math]}$ a%，但9月整体月销售总量仍比（1）问中的计划销售总量上涨a%，其中线下销售量占到了9月总销售量的 $\text{[math]}$ ，最终9月总销售额比8月增加了 $\text{[math]}$ a元，求a的值．
答案解析收藏纠错 + 选题
22. (2022·新余模拟) 综合与实践
如图1，已知点G在正方形ABCD的对角线AC 上，GE⊥BC，垂足为E，GF⊥CD，垂足为F．
1. （1）（证明与推断）
  ①四边形CEGF的形状是；
  
  ② $\text{[math]}$ 的值为；
2. （2）（探究与证明）
  在图1的基础上，将正方形CEGF绕点C按顺时针方向旋转α角（0°<α<45°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；
3. （3）（拓展与运用）
  如图3，在（2）的条件下，正方形CEGF 在旋转过程中，当B、E、F三点共线时，探究AG和GE的位置关系，并说明理由．
答案解析收藏纠错 + 选题
23. (2021九上·灵石期中) 如图，在平面直角坐标系中，直线y= $\text{[math]}$ x+1与x轴交于点A，与y轴交于点C，点B （4，3）是直线上的一点．
1. （1）求A点和C点的坐标．
2. （2）已知x轴上一动点P（m，0），连接BP，若△ABP与△AOC相似，求m的值．
3. （3）设直线x= $\text{[math]}$ 与BC交于点M，点N是直线x= $\text{[math]}$ 上任意一点，且点M 与点N不重合，是否存在点N，使得以M、B、N为顶点的三角形与△AOC相似．若存在，请直接写出N点的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题