![]()

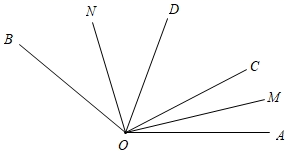
①比较线段的大小:
(填:“>”、“=”或“<”);
②若 ,
,M是
的中点, N是
的中点,求
的长度.

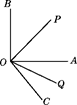




(ⅱ)若 ,求
的度数.
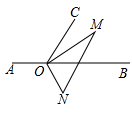
①作射线 ,过点
作直线
,使
两点在直线
两旁;
②过点 作直线
的垂线段,垂足为
;
③点 为直线
上任意一点,点
为射线
上任意一点,连结线段
.

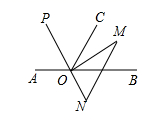


①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CF=3,求AD的长;

