北京市21、22中联盟校2021-2022学年九年级上学期1...

更新时间：2022-01-27 浏览次数：135 类型：月考试卷

一、单选题

1. (2021九上·北京市月考) 下列方程中一元二次方程的个数为（）
①2x²－3＝0； ②x²＋y²＝5； ③ $\text{[math]}$ ； ④ $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2021九上·北京市月考) 下列叙述正确的是（）

A . 形如 $\text{[math]}$ 的方程叫一元二次方程 B . 方程 $\text{[math]}$ 不含有常数项 C . 一元二次方程中，二次项系数、一次项系数及常数项均不能为0 D . $\text{[math]}$ 是关于y的一元二次方程

答案解析收藏纠错 + 选题
3. 如图，△ABC经过变换得到△AB'C'，其中△ABC绕点A逆时针旋转60°的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023九上·延吉期末) 抛物线y＝（x﹣1）²+3的顶点坐标是（）

A . （1，3） B . （﹣1，3） C . （1，﹣3） D . （3，﹣1）

答案解析收藏纠错 + 选题
5. (2022八下·临淄期中) 已知关于x的一元二次方程x²+bx﹣1＝0，则下列关于该方程根的判断，正确的是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 实数根的个数与实数b的取值有关

答案解析收藏纠错 + 选题

6. (2021九上·北京市月考) 老师给出了二次函数y＝ax²＋bx＋c（a≠0）的部分对应值如表：

x	…	﹣3	﹣2	0	1	3	5	…
y	…	7	0	﹣8	﹣9	﹣5	7	…

同学们讨论得出了下列结论，

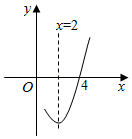
①抛物线的开口向上；②抛物线的对称轴为直线x＝2；③当﹣2＜x＜4时，y＜0；④当x＞1时，y随x的增大而增大；⑤若方程ax²＋bx＋c＝m有两个不相等的实数根，则m＞﹣9．

其中正确的个数是（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

7. (2021九上·北京市月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点C逆时针旋转得到 $\text{[math]}$ ，点A，B的对应点分别为D，E，连接 $\text{[math]}$ ．当点A，D，E在同一条直线上时，下列结论一定正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·北京市月考) 跳台滑雪是冬季奥运会比赛项目之一．运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度 $\text{[math]}$ （单位： $\text{[math]}$ ）与水平距离 $\text{[math]}$ （单位： $\text{[math]}$ ）近似满足函数关系 $\text{[math]}$ （ $\text{[math]}$ ）．下图记录了某运动员起跳后的 $\text{[math]}$ 与 $\text{[math]}$ 的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021九上·北京市月考) 如图，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，若 $\text{[math]}$ 且 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

10. (2024九下·西安模拟) 一元二次方程x²﹣4x+4=0的解是．

答案解析收藏纠错 + 选题
11. (2021八下·余杭期中) 已知m是关于x的方程x²﹣3x﹣4＝0的一个根，则3m²﹣9m﹣2＝．

答案解析收藏纠错 + 选题
12. (2021九上·北京市月考) 若二次函数y＝2x²－3的图象上有两个点A(1，m)，B(2，n)，则mn(填“<”“＝”或“>”)．

答案解析收藏纠错 + 选题
13. (2021九上·余干期中) 如图， $\text{[math]}$ ABC的三个顶点都在方格纸的格点上，其中A点的坐标是 $\text{[math]}$ ，现将 $\text{[math]}$ ABC绕A点按逆时针方向旋转 $\text{[math]}$ ，则旋转后点C对应点的坐标是．

答案解析收藏纠错 + 选题
14. (2021九上·北京市月考) 如图，抛物线 $\text{[math]}$ 的对称轴为 $\text{[math]}$ ，点P，点Q是抛物线与x轴的两个交点，若点P的坐标为（4，0），则点Q的坐标为．

答案解析收藏纠错 + 选题
15. (2021九上·南京月考) 已知抛物线y＝ax²+bx+c的对称轴为直线x＝2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b＝0；③a﹣b+c＜0；④b²＞4ac；⑤当x＜2时，y随x的增大而增大，你认为其中正确的是 .（填序号）

答案解析收藏纠错 + 选题
16. (2021九上·北京市月考) 定义：若抛物线与x轴有两个交点，且这两个交点与它的顶点所构成的三角形是直角三角形，则把这种抛物线称作“和美抛物线”.如图，一组抛物线的顶点B₁(1，y₁)，B₂(2，y₂)，B₃(3，y₃)，… B_n(n，y_n)（n为正整数）依次是直线y $\text{[math]}$ 上的点，这组抛物线与x轴正半轴的交点依次是A₁(a₁ ， 0)，A₂(a₂ ， 0)，A₃(a₃ ， 0)，…A_n+1(a_n+1 ， 0)（0＜a₁＜1，n为正整数）.若这组抛物线中存在和美抛物线，则a₁＝.

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·北京市月考) 解方程：
1. （1） $\text{[math]}$
2. （2） 6x²－x－2＝0．
答案解析收藏纠错 + 选题
18. (2021九上·北京市月考) 如图，方格纸中的每个小方格都是边长为1个单位的正方形，建立如图所示的平面直角坐标系， $\text{[math]}$ 的顶点均在格点上，点 $\text{[math]}$ 的坐标为（1，0）．
1. （1）画出将 $\text{[math]}$ 绕原点 $\text{[math]}$ 按顺时针旋转90°所得的 $\text{[math]}$ ，并写出 $\text{[math]}$ 点的坐标．
2. （2）求线段 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
19. (2021九上·北京市月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ .将 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转后得 $\text{[math]}$ ，连接 $\text{[math]}$ .当 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数.

答案解析收藏纠错 + 选题
20. (2021九上·北京市月考) 已知抛物线C₁：y＝（x+2）²﹣1，抛物线C₁ ，的顶点为A，与y轴的交点为B．

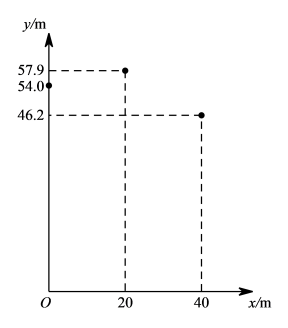
⑴点A的坐标是 ▲ ，点B的坐标是 ▲ ；

⑵在平面直角坐标系中画出C₁的图象（不必列表）；

⑶将抛物线C₁向下平移3个单位，向右平移2个单位后得到抛物线C₂ ，画出平移后的抛物线C₂并写出抛物线C₂的解析式．

答案解析收藏纠错 + 选题
21. (2021九上·北京市月考) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个不相等的实数根．
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）若 $\text{[math]}$ 为满足条件的最大整数，求方程的根．
答案解析收藏纠错 + 选题
22. (2021九上·大兴期末) 某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w（双）与销售单价x（元）满足w＝﹣2x+80（20≤x≤40），设销售这种手套每天的利润为y（元）．
1. （1）求y与x之间的函数关系式；
2. （2）当销售单价定为多少元时，每天的利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
23. (2021九上·北京市月考) 有这样一个问题：探究函数y= $\text{[math]}$ （x﹣1）（x﹣2）（x﹣3）+x的性质．
1. （1）先从简单情况开始探究：
  ①当函数y= $\text{[math]}$ （x﹣1）+x时，y随x增大而（填“增大”或“减小”）；
  ②当函数y= $\text{[math]}$ （x﹣1）（x﹣2）+x时，它的图象与直线y=x的交点坐标为；
2. （2）当函数y= $\text{[math]}$ （x﹣1）（x﹣2）（x﹣3）+x时，
  下表为其y与x的几组对应值．
  x
  …
  ﹣ $\text{[math]}$
  0
  1
  $\text{[math]}$
  2
  $\text{[math]}$
  3
  4
  $\text{[math]}$
  …
  y
  …
  ﹣ $\text{[math]}$
  ﹣3
  1
  $\text{[math]}$
  2
  $\text{[math]}$
  3
  7
  $\text{[math]}$
  …
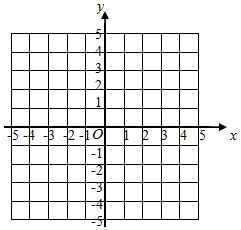
  ①如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，请根据描出的点，画出该函数的图象；
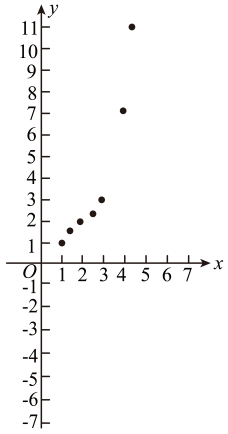
  ②根据画出的函数图象，写出该函数的一条性质： ▲ ．
答案解析收藏纠错 + 选题
24. (2021九上·北京市月考) 随着国内新能源汽车的普及，为了适应社会的需求，全国各地都在加快公共充电桩的建设，某省2018年公共充电桩的数量为2万个，2020年公共充电桩的数量为2.88万个．
1. （1）求2018年至2020年该省公共充电桩数量的年平均增长率；
2. （2）按照这样的增长速度，预计2021年该省将新增多少万个公共充电桩？
答案解析收藏纠错 + 选题
25. (2023九上·广州月考) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ ．
1. （1）求证：该方程总有两个实数根；
2. （2）若 $\text{[math]}$ ，且该方程的两个实数根的差为2，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
26. (2021九上·宁明期中) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于两点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值．
2. （2）观察函数的图象，直接写出当 $\text{[math]}$ 取何值时， $\text{[math]}$ ．
3. （3）设抛物线交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，在该抛物线的对称轴上是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ 的周长最小？若存在，求出 $\text{[math]}$ 点的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
27. (2021九上·北京市月考) 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，①求抛物线G与x轴的交点坐标；
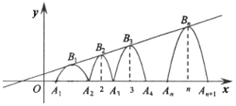
  ②若抛物线G与线段 $\text{[math]}$ 只有一个交点，求n的取值范围；
2. （2）若存在实数a，使得抛物线G与线段 $\text{[math]}$ 有两个交点，结合图象，直接写出n的取值范围．
答案解析收藏纠错 + 选题
28. (2021九上·北京市月考) 定义：若关于x的一元二次方程ax²+bx+c＝0（a≠0）的两个实数根为x₁ ， x₂（x₁＜x₂），分别以x₁ ， x₂为横坐标和纵坐标得到点M（x₁ ， x₂），则称点M为该一元二次方程的衍生点．
1. （1）若方程为x²﹣2x＝0，写出该方程的衍生点M的坐标．
2. （2）若关于x的一元二次方程x²﹣（2m+1）x+2m＝0（m＜0）的衍生点为M，过点M向x轴和y轴作垂线，两条垂线与坐标轴恰好围成一个正方形，求m的值．
3. （3）是否存在b，c，使得不论k（k≠0）为何值，关于x的方程x²+bx+c＝0的衍生点M始终在直线y＝kx﹣2（k﹣2）的图象上，若有请直接写出b，c的值，若没有说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北京市21、22中联盟校2021-2022学年九年级上学期1...

副标题：

*注意事项：

北京市21、22中联盟校2021-2022学年九年级上学期1...

试题分析

总体分析

题量分析

难度分析

知识点分析

x	…	﹣ $\text{[math]}$	0	1	$\text{[math]}$	2	$\text{[math]}$	3	4	$\text{[math]}$	…
y	…	﹣ $\text{[math]}$	﹣3	1	$\text{[math]}$	2	$\text{[math]}$	3	7	$\text{[math]}$	…