浙江省金华市第五中学2021-2022学年九年级上学期12月...

更新时间：2024-07-31 浏览次数：82 类型：月考试卷

一、单选题

1. (2021九上·金华月考) －2×3＝（）

A . －8 B . －6 C . －5 D . － $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·金华月考) 已知直线m∥n，将一块含30°角的直角三角板按如图所示方式放置（∠ABC＝30°），并且顶点A，C分别落在直线m，n上，若∠1＝38°，则∠2的度数是（　　）

A . 20° B . 22° C . 28° D . 38°

答案解析收藏纠错 + 选题
3. (2021九上·金华月考) 不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九下·淮南月考) 如图，在△ABC中，∠C=90°，AB=5 ，BC=3，则tanB的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九上·金华月考) 有颜色不同的15个红球和若干个白球装在不透明的袋子里，从袋子里摸出一个球记录下颜色后放回，经过多次重复试验，发现摸到白球的频率稳定在0.4，则袋中白球有（）

A . 10个 B . 16个 C . 24个 D . 40个

答案解析收藏纠错 + 选题
6. (2021九上·金华月考) 若m是方程x²＋x﹣1＝0的根，则2m²＋2m＋2020的值为（）

A . 2022 B . 2021 C . 2020 D . 2019

答案解析收藏纠错 + 选题
7. (2021九上·科尔沁期末) 如图，圆锥侧面展开得到扇形，此扇形半径 $\text{[math]}$ ，圆心角 $\text{[math]}$ ，则此圆锥高 $\text{[math]}$ 的长度是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·金华月考) 已知一次函数y₁=x－1和反比例函数y₂= $\text{[math]}$ 的图象在平面直角坐标系中交于A、B两点，当y₁＞y₂时，x的取值范围是（）

A . x＞2 B . －1＜x＜0 C . x＞2，－1＜x＜0 D . x＜2，x＞0

答案解析收藏纠错 + 选题
9. (2021九上·金华月考)
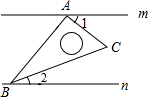
足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在（）

A . 点C B . 点D或点E C . 线段DE（异于端点）上一点 D . 线段CD（异于端点）上一点

答案解析收藏纠错 + 选题
10. (2021九上·金华月考) 如图， $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形，且 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的边长为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·金华月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的补角等于．

答案解析收藏纠错 + 选题
12. (2021九上·金华月考) 若a＋b＝3，ab＝1，则（a﹣b）²＝.

答案解析收藏纠错 + 选题
13. (2021九上·金华月考) 由于木质衣架没有柔性，在挂置衣服的时候不太方便操作.小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可.如图2，衣架杆 $\text{[math]}$ ，若衣架收拢时， $\text{[math]}$ ，如图1，若衣架打开时， $\text{[math]}$ ，则此时 $\text{[math]}$ ， $\text{[math]}$ 两点之间的距离扩大了 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2021九上·金华月考) 如图，在半径为 $\text{[math]}$ 的⊙O中，弦 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是.

答案解析收藏纠错 + 选题
15. (2021九上·金华月考) 如图，点D是平行四边形OABC内一点，CD与x轴平行，BD与y轴平行，BD＝ $\text{[math]}$ ，∠ADB＝135°，S_△ABD＝2，若反比例函数y＝ $\text{[math]}$ （x＞0）的图象经过A、D两点，则k的值是

答案解析收藏纠错 + 选题
16. (2021九上·金华月考) 图1是一种指甲剪.该指甲剪利用杠杆原理操作，使用者只需施力按压柄的末端，便可轻易透过锋利的前端刀片剪断指甲，它被按压后示意图如图2所示，上下臂 $\text{[math]}$ $\text{[math]}$ 杠杆 $\text{[math]}$ 轴承 $\text{[math]}$ ，未使用指甲剪时，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ 比 $\text{[math]}$ 长 $\text{[math]}$ ，则 $\text{[math]}$ 的长为 $\text{[math]}$ ；使用指甲剪时，下压点 $\text{[math]}$ ，当 $\text{[math]}$ 时，两刀片咬合， $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转到 $\text{[math]}$ 的位置，则 $\text{[math]}$ 与 $\text{[math]}$ 的交点从开始到结束时移动的距离 $\text{[math]}$ 为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·金华月考) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021九上·金华月考) 解分式方程： $\text{[math]}$

答案解析收藏纠错 + 选题
19. 如图，在 $\text{[math]}$ 的正方形网格中，每个小正方形的边长均为1，且每个小正方形的顶点称为格点，线段 $\text{[math]}$ 的两个端点均在格点上，按要求完成下列画图．（要求：用无刻度的直尺，保留画图痕迹，不要求写出画法）
1. （1）在图1中，画出一个以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形，且这个三角形的面积为6， $\text{[math]}$ 为格点．
2. （2）在图2中，画出一个以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形，且 $\text{[math]}$ ，点 $\text{[math]}$ 为格点．
3. （3）在图3中，画出一个既是中心对称，又是轴对称，且以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形，其邻边之比为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为格点．
答案解析收藏纠错 + 选题
20. (2021九上·金华月考) 图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框
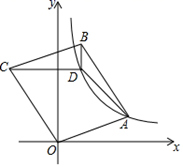
上，通过推动左侧活页门开关；图2是其俯视图简化示意图，已知轨道 $\text{[math]}$ ，两扇活页门的宽 $\text{[math]}$ ，点 $\text{[math]}$ 固定，当点 $\text{[math]}$ 在 $\text{[math]}$ 上左右运动时， $\text{[math]}$ 与 $\text{[math]}$ 的长度不变(所有结果保留小数点后一位).
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）当点 $\text{[math]}$ 从点 $\text{[math]}$ 向右运动60 $\text{[math]}$ 时，求点 $\text{[math]}$ 在此过程中运动的路径长.
  （参考数据：sin50°≈0.77， cos50°≈0.64， tan50°≈1.19， π取3.14）
答案解析收藏纠错 + 选题
21. (2021九上·金华月考) 我区某校采用随机抽样的方式对学生掌握安全知识的情况进行书面测评，并按成绩高低分成优、良中差四个等级进行统计，绘制了下面两幅尚不完整的统计图.请根据有关信息解答：
1. （1）接受测评的学生共有人，扇形统计图中“优”部分所对应扇形的圆心角为 $\text{[math]}$ ，并补全条形统计图；
2. （2）若该校共有学生2800人，请估计该校学生对安全知识达到“良”及“良”级以上程度的人数；
3. （3）测评成绩前五名的学生恰好是3个女生和2个男生，现从中随机抽取2人代表学校参加区级安全知识竞赛，求出抽到的2个学生恰好是一男生与一女生的概率.
答案解析收藏纠错 + 选题
22. (2021九上·金华月考) 在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D，⊙O的切线BP与AC的延长线交于点P，连接DE，BE.
1. （1）求证：BD=DE；
2. （2） ∠AED=∠BCP；
3. （3）已知：sin∠BAD= $\text{[math]}$ ，AB=10，求AP的长.
答案解析收藏纠错 + 选题
23. (2021九上·金华月考) 如图，直线 $\text{[math]}$ 交y轴于点A，交x轴于点C，抛物线 $\text{[math]}$ 经过点A，点C，且交x轴于另一点B.
1. （1）求抛物线的表达式；
2. （2）在直线 $\text{[math]}$ 上方的抛物线上有一点M，求使四边形 $\text{[math]}$ 的面积最大值时点M的坐标；
3. （3）
  将线段OA绕线段OC上的一动点P（m，0）顺时针旋转90°得到线段O'A'，若线段O'A'与抛物线只有一个公共点，请结合函数图象，求m的取值范围.
答案解析收藏纠错 + 选题
24. (2021九上·金华月考) 如图，在Rt△ABC中，∠ACB＝90°，AC＝6，∠ABC＝30°，点D，E分别在边AB，AC上，在线段ED左侧构造Rt△DEF，使△DEF∽△BCA .
1. （1）如图1，若AD＝BD，点E与点C重合，DF与BC相交于点H.求证：2CH＝BH.
2. （2）当AE＝2时，连接BF，取BF的中点G，连接DG.
  ①如图2，若点F落在AC边上，求DG的长.
  ②是否存在点D，使得△DFG是直角三角形？若存在，求AD的长；若不存在，试说明理由.
答案解析收藏纠错 + 选题