浙江省温州市实验中学2021-2022学年九年级上学期12月...

更新时间：2022-03-11 浏览次数：86 类型：月考试卷

一、单选题

1. (2021九上·温州月考) 已知⊙O的半径为5，若点P在⊙O内，则OP的长可以是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
2. (2021九上·温州月考) 二次函数 $\text{[math]}$ 的对称轴为（）

A . 直线x＝5 B . 直线x＝2 C . 直线x＝﹣2 D . 直线x＝﹣5

答案解析收藏纠错 + 选题
3. (2021九上·温州月考) 已知点P是线段AB的黄金分割点，AP＞PB.若AB＝2，则AP的长为（）

A . $\text{[math]}$ B . 3﹣ $\text{[math]}$ C . $\text{[math]}$ ﹣1 D . $\text{[math]}$ ﹣3

答案解析收藏纠错 + 选题
4. (2021九上·温州月考) 如图，点A，B，C在⊙O上，若∠ACB＝40°，则∠AOB的度数为（）

A . 40° B . 45° C . 50° D . 80°

答案解析收藏纠错 + 选题
5. (2021九上·温州月考) 在一个不透明的袋中装有仅颜色不同的白球和红球共20个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球，记下颜色后再放回袋中；然后重复上述步骤……如表是实验中记录的部分统计数据：
摸球次数
10
40
80
200
500
800
摸到红球次数
3
16
20
40
100
160
摸到红球的频率
0.3
0.4
0.25
0.2
0.2
0.2
则袋中的红球个数可能有（）

A . 16个 B . 8个 C . 4个 D . 2个

答案解析收藏纠错 + 选题
6. (2021九上·温州月考) 已知二次函数y＝ax²+bx+c的部分图象如图，则关于x的一元二次方程ax²+bx+c＝0的解为（）

A . x₁＝﹣4，x₂＝2 B . x₁＝﹣3，x₂＝﹣1 C . x₁＝﹣4，x₂＝﹣2 D . x₁＝﹣2，x₂＝2

答案解析收藏纠错 + 选题
7. (2021九上·温州月考) 如图，点E，D，F在△ABC的三边上，四边形AEDF是菱形，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·普陀期末) 如图，小王在高台上的点A处测得塔底点C的俯角为α，塔顶点D的仰角为β，已知塔的水平距离AB＝a，则此时塔高CD的长为（）

A . asinα+asin β B . atanα+atan β C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021九上·温州月考) 小明设计了如图所示的树型图案，它是由4个正方形、8个等边三角形和5个扇形组成，其中正方形的边长、等边三角形的边长和扇形的半径均为3，则图中扇形的弧长总和为（）

A . 8π B . $\text{[math]}$ π C . $\text{[math]}$ π D . 12π

答案解析收藏纠错 + 选题
10. (2021九上·温州月考) 如图，Rt△ABC中，∠ACB＝90°，分别以AB，BC，AC为边在△ABC外部作正方形ADEB，CBFG，ACHI.将正方形ABED沿直线AB翻折，得到正方形ABE'D'，AD'与CH交于点N，点E'在边FG上，D'E'与CG交于点M，记△ANC的面积为S₁ ，四边形 $\text{[math]}$ 的面积为S₂ ，若CN＝2NH，S₁+S₂＝14，则正方形ABED的面积为（）

A . 25 B . 26 C . 27 D . 28

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·福田期中) 若3x＝7y，则 $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
12. (2021九上·温州月考) 某商场举办有奖购物活动，购货满100元者发兑奖券一张，每张奖券获奖的可能性相同.在100张奖券中，设一等奖5个，二等奖10个，三等奖20个.若小李购货满100元，则她获奖的概率为 .

答案解析收藏纠错 + 选题
13. (2021九上·温州月考) 将抛物线y＝x²向左平移3个单位，再向下平移2个单位得到的抛物线解析式为 .

答案解析收藏纠错 + 选题
14. (2022九上·拱墅月考) 如图，已知正方形ABCD和正△EGF都内接于⊙O，当EF∥BC时， $\text{[math]}$ 的度数为 .

答案解析收藏纠错 + 选题
15. (2021九上·温州月考) 如图，在△ABC中，AB＝AC＝10，AD⊥BC于点D，AD＝8，若点E是△ABC的重心，点F是△ACD的重心，则△AEF的面积为 .

答案解析收藏纠错 + 选题
16. (2021九上·温州月考) 助推轮椅可以轻松解决起身困难问题.如图1是简易结构图，该轮椅前⊙O₁和后轮⊙O₂的半径分别为0.6dm和3dm，竖直连接处CO₁＝1dm，水平连接处BD与拉伸装置DE共线，BD＝2dm，座面GF平行于地面且GF＝DE＝4.8dm，HF是轮椅靠背，∠ADE始终保持角度不变.初始状态时，拉伸杆AD的端点A在点B正上方且距地面2.2dm，则tan∠ADB的值为 .如图2，踩压拉伸杆AD，装置随之运动，当AD踩至与BD重合时，点E，F，H分别运动到点E'，F'，H'，此时座面GF'和靠背F'H'连成一直线，点H运动到最高点H'，且H'，F，O₂三点正好共线，则H'O₂的长为 dm.

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·普陀期末) 计算：
1. （1） $\text{[math]}$ .
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2021九上·温州月考) 小王和小刘两人在玩转盘游戏时，游戏规则：同时转动A，B两个转盘，当两转盘停止后，若指针所指两个区域的数字之和为2的倍数，则小王获胜；若指针所指两个区域的数字之积为2的倍数，则小刘获胜，如果指针落在分割线上，则视为无效，需重新转动转盘.
1. （1）请用列表或画树状图的方法表示所有可能的结果.
2. （2）这个游戏规则对双方公平吗？请说明理由.
答案解析收藏纠错 + 选题
19. (2021九上·温州月考) 如图，在▱ABCD中，过B作BE⊥CD于点E，连结AE，F为AE上一点，且∠AFB＝∠D.
1. （1）求证：△ABF∽△EAD.
2. （2）若 $\text{[math]}$ ， AD＝6，∠BAE＝30°，求BF的长.
答案解析收藏纠错 + 选题
20. (2021九上·温州月考) 如图，在6×6的方格纸ABCD中给出格点O和格点△EFG，请按要求画格点三角形（顶点在格点上）.
1. （1）在图1中画格点△OPQ，使点P，Q分别落在边AD，BC上，且∠POQ＝90°；
2. （2）在图2中画格点△GMN，使它与△EFG相似（但不全等）.
答案解析收藏纠错 + 选题
21. (2021九上·温州月考) 如图，已知抛物线y＝x²+bx+c经过A（﹣1，0），B（3，0）两点.
1. （1）求抛物线的解析式及顶点C坐标；
2. （2）直线l交抛物线于点D（﹣2，m），E（m，n）.若点P在抛物线上且在直线l下方（不与点D，E重合），求点P纵坐标的取值范围.
答案解析收藏纠错 + 选题
22. (2021九上·温州月考) 定义：如果一个三角形一条边上的高与这条边的比值叫做这条边所对角的准对（记作qad）.如图1，在△ABC中，AH⊥BC于点H，则qad∠BAC＝ $\text{[math]}$ .当qad∠BAC＝ $\text{[math]}$ 时，则称∠BAC为这个三角形的“金角”.已知在矩形ABCD中，AB＝3，BC＝6，△ACE的“金角”∠EAC所对的边CE在BC边上，将△ACE绕点C按顺时针方向旋转α（0°＜α＜90°）得到△A'CE'，A'C交AD边于点F.
1. （1）如图2，当α＝45°时，求证：∠ACF是“金角”.
2. （2）如图3，当点E'落在AD边上时，求qad∠AFC的值.
答案解析收藏纠错 + 选题
23. (2021九上·温州月考) 某企业决定从甲、乙两种产品中选择一种生产，打入国际市场，已知生产销售这两种产品的有关数据如表：（单位：万元）

年固定成本
每件产品成本
每件产品销售价
甲产品
20
a
10
乙产品
40
8
18
a为常数，且3≤a≤8.甲产品每年最多可生产销售200件，乙产品每年最多可生产销售80件，销售乙产品x件时需另外上交0.05x²万元的特别关税.
1. （1）写出该企业生产销售乙产品的年利润y关于x的函数表达式为.
2. （2）当销售乙产品多少件时，可获乙产品的利润最大？最大利润是多少？
3. （3）该企业选择哪一种产品生产销售可获得最大年利润？请说明理由.
答案解析收藏纠错 + 选题
24. (2021九上·温州月考) 如图，四边形ABCD内接于⊙O，AB为直径，连结AC，BD交于点E，弦CF⊥BD于点G，连结AG，且满足∠1＝∠2.
1. （1）求证：四边形AGCD为平行四边形.
2. （2）设tanF＝x，tan∠3＝y，
  ①求y关于x的函数表达式.
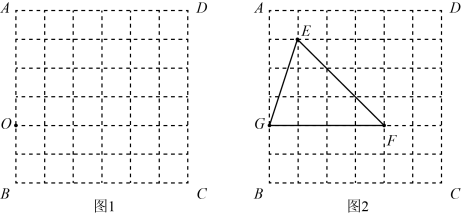
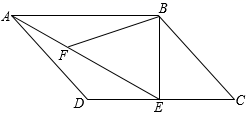
  ②已知⊙O的直径为2 $\text{[math]}$ ， y＝ $\text{[math]}$ ，点H是边CF上一动点，若AF恰好与△DHE的某一边平行时，求CH的长.
  ③连结OG，若OG平分∠DGF，则x的值为 ▲ .
答案解析收藏纠错 + 选题