2021-2022学年浙教版数学七下2.5 三元一次方程组及...

更新时间：2022-02-07 浏览次数：142 类型：同步测试

一、单选题

1. (2021七下·防城月考) 方程组 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021七下·长寿期末) 若实数 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定值

答案解析收藏纠错 + 选题
3. (2021七下·遂宁期末) 若 $\text{[math]}$ ， $\text{[math]}$ ，则x＋y＋z的值等于（）

A . 0 B . 2 C . 1 D . 无法求出

答案解析收藏纠错 + 选题
4. (2021八上·温岭竞赛) 有铅笔、练习本、圆珠笔三种学习用品．若购铅笔3支，练习本7本，圆珠笔1支共需31元；若购铅笔4支，练习本10本，圆珠笔1支共需42元．现购铅笔，练习本，圆珠笔各1个，共需（）

A . 12元 B . 10.5元 C . 9.5元 D . 9元

答案解析收藏纠错 + 选题
5. (2022七下·隆昌月考) 6月18日最开始是京东的周年庆，相当于淘宝的双十一活动，在2013年之前，京东就将每年的6月18日定为年庆。2013年后，618就成了各大电商平台的网购节了。在618当日，小李在某电商平台上选择了甲乙丙三种商品，当购物车内选3件甲，2件乙，1件丙时显示价格为420元；当选2件甲，3件乙，4件丙时显示价格为580元，那么购买甲、乙、丙各一件时应该付款（）

A . 580元 B . 500元 C . 420元 D . 200元

答案解析收藏纠错 + 选题
6. (2022七下·湘桥期末) 甲、乙、丙三种商品，若购买甲2件、乙4件、丙3件，共需220元钱，购甲3件、乙1件、丙2件共需235元钱，那么购甲、乙、丙三种商品各一件共需（）

A . 85元 B . 89元 C . 90元 D . 91元

答案解析收藏纠错 + 选题
7. (2021七下·杭州期中) 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密）（解密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c，对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（）

A . 6，2，7 B . 2，6，7 C . 6，7，2 D . 7，2，6

答案解析收藏纠错 + 选题
8. (2021七下·射洪月考) 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，购买方案有（）

A . 12种 B . 14种 C . 15种 D . 16种

答案解析收藏纠错 + 选题
9. (2022七下·金华月考) 某宾馆有单人间，双人间，三人间三种客房供游客选择居住，现某旅游团有20名旅客同时安排游客居住在该宾馆，若每个房间都住满，共租了9间客房，则居住方案（）

A . 1种 B . 2种 C . 3种 D . 4种

答案解析收藏纠错 + 选题
10. (2024七上·长兴期末) 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上，小明站立在地面上（如图1），然后交换位置（如图2），测量的数据如图所示，想要探究的问题有：①小明的身高；②小亮的身高；③箱子的高度；④小明与小亮的身高和.根据图上信息，你认为可以计算出的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题

二、填空题

11. (2021七下·巴南期末) “端午节”是我国的传统佳节，民间历来有吃粽子的习俗.某超市准备了515个豆沙粽，525个火腿粽和若干个腊肉棕，将这些粽子分成了A，B，C三类礼品盒进行包装.A类礼品盒里有4个豆沙粽，4个火腿粽和6个腊肉粽；B类礼品盒里有3个豆沙粽，5个火腿粽和6个腊肉粽；C类礼品盒里有6个豆沙粽，4个火腿粽和4个腊肉粽.已知A，B，C三类礼品盒的数量都为正整数，并且A类礼品盒少于44盒，B类礼品盒少于49盒.如果所有礼品盒里的腊肉粽的总个数为m，则m=

答案解析收藏纠错 + 选题
12. (2021八下·綦江期末) 全球棉花看中国，中国棉花看新疆．新疆长绒棉花是世界顶级棉花，品质优，产量大，常年供不应求．綦江区某超市为了支持新疆棉花，在“五一节”进行促销活动，将新疆棉制成 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三种品牌毛巾混装成甲、乙、丙三种礼包销售，其中甲礼包含1条 $\text{[math]}$ 品牌毛巾、2条 $\text{[math]}$ 品牌毛巾；乙礼包含2条 $\text{[math]}$ 品牌毛巾、2条 $\text{[math]}$ 品牌毛巾， 2条 $\text{[math]}$ 品牌毛巾；丙礼包含2条 $\text{[math]}$ 品牌毛巾、2条 $\text{[math]}$ 品牌毛巾，每个礼包的售价等于礼包各条毛巾售价之和，5月1日当天，超市对 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个品牌毛巾的售价分别打8折、 $\text{[math]}$ 折、 $\text{[math]}$ 折销售，5月2日恢复原价，小明发现5月1日一个甲礼包的售价等于5月2日一个乙礼包售价的 $\text{[math]}$ ，5月1日一个乙礼包的售价比5月2日一个丙礼包售价少2.4元，若 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个品牌的毛巾原价都是正整数，且 $\text{[math]}$ 品牌毛巾的原价不超过14元，则小明在5月1日购买的二个甲礼包和一个乙礼包，应该付元．

答案解析收藏纠错 + 选题
13. (2021七下·苏州期末) “洞庭碧螺春，品香醉天下.”洞庭碧螺春产于苏州市太湖洞庭山，以形美、色艳、香浓、味醇“四绝”驰名中外.如图，若将一壶碧螺春茶倒满2个小杯，则还剩 $\text{[math]}$ 壶；若倒满1个小杯后再全部倒入1个大杯中，则只能倒满这个大杯的 $\text{[math]}$ .1个小杯与1个大杯的容积之比为.

答案解析收藏纠错 + 选题
14. (2021七下·卧龙期末) 如图，在正方形 $\text{[math]}$ 的每个顶点上写一个数，然后把它的每条边的两个端点上的数加起来，将结果写在这条边上，若 $\text{[math]}$ 边上的数字是3， $\text{[math]}$ 边上的数字是7， $\text{[math]}$ 边上的数字是10，则 $\text{[math]}$ 边上的数字是.

答案解析收藏纠错 + 选题
15. (2021七下·万州期末) 农历五月初五，中国传统节日端午节.某超市为了吸引顾客，在端午节当天推出由白粽、豆沙粽、蛋黄粽三种不同的粽子搭配而成的A、B两种礼盒，其中，A种礼盒含4个白粽、3个豆沙粽、3个蛋黄粽；B种礼盒含2个白粽、4个豆沙粽、4个蛋黄粽.每种礼盒的成本价分别为三种粽子的成本价之和（包装成本忽略不计），已知每盒A种礼盒的总成本为1个白粽成本的13倍，每盒A种礼盒的利润率为20%，每盒B种礼盒的利润率为25%，则当销售A、B两种礼盒的数量之比为7：26时，则该超市销售这两种礼盒的总利润率为.

答案解析收藏纠错 + 选题
16. (2021七下·渝北期末) “吃了端午粽，才把棉衣送”，每逢农历的五月初五端午节，大家都会阖家团聚，品尝端午粽，尽享天伦之乐.今年端午节前夕某商场结合当地的情况，对A， $\text{[math]}$ ， $\text{[math]}$ 三种粽子进行搭配销售，并推出甲、乙两种盒装粽子，每一种盒装粽子的成本是该盒中所有A， $\text{[math]}$ ， $\text{[math]}$ 三种粽子的成本之和（盒子的费用不计）.每盒甲由3个A，1个 $\text{[math]}$ ，1个 $\text{[math]}$ 组成；每盒乙由2个A，3个 $\text{[math]}$ ，3个 $\text{[math]}$ 组成.每盒甲中所有A， $\text{[math]}$ ， $\text{[math]}$ 的成本之和是1个A成本的4倍，每盒乙的利润率为20%，每盒乙的售价比每盒甲的售价高20%.该商场在端午节这天销售这两种盒装粽子的总销售额为14700元，总利润率为22.5%.则该商场在端午节这天销售甲种盒装粽子的总利润是元.

答案解析收藏纠错 + 选题

三、综合题

17. (2021七下·吴中期末) 对于未知数为 $\text{[math]}$ ， $\text{[math]}$ 的二元一次方程组，如果方程组的解 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，我们就说方程组的解 $\text{[math]}$ 与 $\text{[math]}$ 具有“邻好关系”.
1. （1）方程组 $\text{[math]}$ 的解 $\text{[math]}$ 与 $\text{[math]}$ 是否具有“邻好关系”?说明你的理由：
2. （2）若方程组 $\text{[math]}$ 的解 $\text{[math]}$ 与 $\text{[math]}$ 具有“邻好关系”，求 $\text{[math]}$ 的值：
3. （3）未知数为 $\text{[math]}$ ， $\text{[math]}$ 的方程组 $\text{[math]}$ ，其中 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 都是正整数，该方程组的解 $\text{[math]}$ 与 $\text{[math]}$ 是否具有“邻好关系”?如果具有，请求出 $\text{[math]}$ 的值及方程组的解：如果不具有，请说明理由.
答案解析收藏纠错 + 选题
18. (2021七下·盐城期末) （阅读感悟）
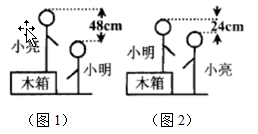
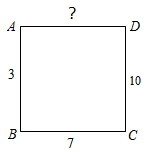
对于方程组的问题，有时候要求的结果不是每个未知数的值，而是求关于未知数的代数式的值.如已知实数 $\text{[math]}$ 、 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的值.

方法一：解方程组，分别求出 $\text{[math]}$ 、 $\text{[math]}$ 的值，代入代数式求值；

方法二：仔细观察两个方程中未知数的系数之间的关系，通过适当变形整体求代数式的值.解法如下：

①－②，得： $\text{[math]}$ ；①＋②×2，得： $\text{[math]}$ .

比较：方法一运算量较大，是常规思路；方法二运算较为简单，这种解题思路就是通常所说的“整体思想”.

（问题解决）
1. （1）已知二元一次方程组 $\text{[math]}$ ，则 $\text{[math]}$ ； $\text{[math]}$ .
2. （2）某班级因组织活动购买奖品.买13支铅笔、4块橡皮、2本笔记本共需48元；买25支铅笔、7块橡皮、3本笔记本共需84元.则购买5只铅笔、5块橡皮、5本笔记本共需元.
3. （3）对于实数 $\text{[math]}$ 、 $\text{[math]}$ ，定义新运算： $\text{[math]}$ ，其中 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是常数，等式右边是通常的加减法和乘法运算.已知 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的值是.
答案解析收藏纠错 + 选题
19. (2023七上·钦州月考) 对于一个三位数 $\text{[math]}$ ，如果 $\text{[math]}$ 满足：它的百位数字、十位数字之和与个位数字的差等于8，那么称这个数 $\text{[math]}$ 为“快乐数”.例如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是“快乐数”； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 不是“快乐数”.
1. （1）判断844，735是否为“快乐数”？并说明理由；
2. （2）若将一个“快乐数” $\text{[math]}$ 的个位数的3倍放到百位，原来的百位数变成十位数，原来的十位数变成个位数，得到一个新的三位数 $\text{[math]}$ （例如：若 $\text{[math]}$ ，则 $\text{[math]}$ ），若 $\text{[math]}$ 也是一个“快乐数”，求满足条件的所有 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
20. (2021·黄冈模拟) 某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎，每扎1 000张，
已知体彩中心有A、B、C三种不同价格的彩票，进价分别是A彩票每张1.5元，B彩票每张2元，C彩票每张2.5元.
1. （1）若经销商同时购进两种不同型号的彩票20扎，并将45000元恰好用完，请你帮助经销商设计进票方案：
2. （2）若销售A型彩票一张获手续费0.2元，B型彩票一张获手续费0.3元，C型彩票一张获手续费0.5元.在问题(1)设计的购进两种彩票的方案中，为使销售完时获得的手续费最多，你选择哪种进票方案？
3. （3）若经销商准备用45 000元同时购进A、B、C三种彩票20扎，请你帮助经销商设计一种进票方案.（直接写出答案）
答案解析收藏纠错 + 选题
21. (2022七下·隆昌月考) 阅读理解：已知实数x，y满足3x﹣y＝5…①，2x＋3y＝7…②，求x﹣4y和7x＋5y的值.仔细观察两个方程未知数的系数之间的关系，本题可以通过适当变形整体求得代数式的值，如由①﹣②可得x﹣4y＝﹣2，由①＋②×2可得7x＋5y＝19.这样的解题思想就是通常所说的“整体思想”.利用“整体思想”，解决下列问题：
1. （1）已知二元一次方程组 $\text{[math]}$ ，则x﹣y＝，x＋y＝；
2. （2）买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，求购买5支铅笔、5块橡皮5本日记本共需多少元？
3. （3）对于实数x，y，定义新运算：x*y＝ax＋by＋c，其中a，b，c是常数，等式右边是实数运算.已知3*5＝15，4*7＝28，求1*1的值.
答案解析收藏纠错 + 选题
22. (2021八上·永安期末) 有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题∶
已知实数x、y满足 $\text{[math]}$ ①， $\text{[math]}$ ②，求 $\text{[math]}$ 和 $\text{[math]}$ 的值.

本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由① $\text{[math]}$ ②可得 $\text{[math]}$ ，由①＋② $\text{[math]}$ 可得 $\text{[math]}$ .这样的解题思想就是通常所说的“整体思想”.解决问题∶
1. （1）已知二元一次方程组 $\text{[math]}$ 则 $\text{[math]}$ ， $\text{[math]}$ .
2. （2）某班级组织活动购买小奖品，买13支铅笔、5块橡皮、2本日记本共需31元，买25支铅笔、9块橡皮、3本日记本共需55元，则购买3支铅笔、3块橡皮、3本日记本共需多少元？
3. （3）对于实数x、y，定义新运算∶ $\text{[math]}$ ，其中a、b、c是常数，等式右边是通常的加法和乘法运算.已知 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ .
答案解析收藏纠错 + 选题
23. (2021八上·云阳期末) 我国古代民间把正月正、二月二、三月三、五月五、六月六、七月七、九月九这“七重”列为吉庆日；“七”在生活中表现为时间的阶段性，比如一周有“七天”……在数的学习过程中，有一类自然数具有的特性也和“七”有关.
定义：对于四位自然数 $\text{[math]}$ ，若其千位数字与个位数字之和等于7，百位数字与十位数字之和也等于7，则称这个四位自然数 $\text{[math]}$ 为“七巧数”.

例如：3254是“七巧数”，因为 $\text{[math]}$ ， $\text{[math]}$ ，所以3254是“七巧数”； 1456不是“七巧数”，因为 $\text{[math]}$ ，但 $\text{[math]}$ ，所以1456不是“七巧数”.
1. （1）若一个“七巧数”的千位数字为 $\text{[math]}$ ，则其个位数字可表示为（用含 $\text{[math]}$ 的代数式表示）；
2. （2）最大的“七巧数”是，最小的“七巧数”是；
3. （3）若 $\text{[math]}$ 是一个“七巧数”，且 $\text{[math]}$ 的千位数字加上十位数字的和，是百位数字减去个位数字的差的3倍，请求出满足条件的所有“七巧数” $\text{[math]}$ .
答案解析收藏纠错 + 选题
24. (2020·扬州) 阅读感悟：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：

已知实数x、y满足 $\text{[math]}$ ①， $\text{[math]}$ ②，求 $\text{[math]}$ 和 $\text{[math]}$ 的值.

本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由① $\text{[math]}$ ②可得 $\text{[math]}$ ，由① $\text{[math]}$ ② $\text{[math]}$ 可得 $\text{[math]}$ .这样的解题思想就是通常所说的“整体思想”.

解决问题：
1. （1）已知二元一次方程组 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？
3. （3）对于实数x、y，定义新运算： $\text{[math]}$ ，其中a、b、c是常数，等式右边是通常的加法和乘法运算.已知 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ .
答案解析收藏纠错 + 选题
25. (2019七下·广丰期末) 有一场足球比赛，共有九支球队参加，采取单循环赛，其记分和奖励方案如下表：

标准

胜一场

平一场

负一场

积分

3

1

0

奖励（元／人）

2000

800

0

甲队参加完了全部8场比赛，共得积分16分．
1. （1）求甲队胜负的所有可能情况；
2. （2）若每一场比赛，每一个参赛队员均可得出场费500元，求甲队参加了所有8场比赛的队员的个人总收入（奖金加上出场费）．
答案解析收藏纠错 + 选题
26. (2020七下·南安月考) 某货运公司接到 $\text{[math]}$ 吨物资运载任务，现有甲、乙、丙三种车型的汽车供选择，每辆车的运载能力和运费如表：

车型

甲

乙

丙

汽车运载量(吨/辆)

5

8

10

汽车运费(元/辆)

400

500

600
1. （1）甲种车型的汽车 $\text{[math]}$ 辆，乙种车型的汽车 $\text{[math]}$ 辆，丙种车型的汽车 $\text{[math]}$ 辆，它们一次性能运载吨货物．
2. （2）若全部物资都用甲、乙两种车型的汽车来运送，需运费 $\text{[math]}$ 元，求需要甲、乙两种车型的汽车各多少辆？
3. （3）为了节省运费，该公司打算用甲、乙、丙三种车型的汽车共 $\text{[math]}$ 辆同时参与运送，请你帮货运公司设计派车方案；并求出各种派车方案的运费．
答案解析收藏纠错 + 选题