江苏省淮安市洪泽外国语中学2021-2022学年九年级上学期...

更新时间：2022-04-14 浏览次数：117 类型：月考试卷

一、单选题

1. (2021九上·淮安月考) $\text{[math]}$ 的相反数是（）

A . 1 $\text{[math]}$ B . ﹣1 $\text{[math]}$ C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·淮安月考) 下列图形中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022八上·东城期末) 办公中常用的纸张一般A4纸其厚度为0.0075m，将0.0075用科学记数法表示为（）

A . 75×10^﹣4 B . 75×10^﹣3 C . 7.5×10^﹣3 D . 0.75×10^﹣2

答案解析收藏纠错 + 选题
4. (2021九上·滦州期中) 一组数据x、0、1、﹣2、3的平均数是1，则这组数据的中位数是（　　）

A . 0 B . 1 C . 2.5 D . 3

答案解析收藏纠错 + 选题
5. (2023九上·石家庄期中) 如图，由边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB为直径的圆经过点C、D，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·淮安月考) 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021九上·鲁甸期中) 如图，抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，下列结论中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·淮安月考) 小明同学利用计算机软件绘制函数 $\text{[math]}$ （a、b为常数）的图象如图所示，由学习函数的经验，可以推断常数a、b的值满足（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2021八上·南昌期末) 当x＝时，分式 $\text{[math]}$ 的值为0.

答案解析收藏纠错 + 选题
10. (2022八上·上杭期中) 点A（3，﹣2）关于x轴对称的点的坐标是．

答案解析收藏纠错 + 选题
11. (2021九上·淮安月考) 已知反比例函数 $\text{[math]}$ 的图象在一、三象限，则a的取值范围是.

答案解析收藏纠错 + 选题
12. (2021九上·淮安月考) 已知A（﹣4，y₁），B（﹣1，y₂），C（2，y₃）三点都在二次函数y＝2（x+2）²+c的图象上，则y₁ ， y₂ ， y₃的大小关系为 .

答案解析收藏纠错 + 选题
13. (2023九下·兴化月考) 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 $\text{[math]}$ ，该圆锥的母线长 $\text{[math]}$ ，则扇形的圆心角 $\text{[math]}$ 度数为.

答案解析收藏纠错 + 选题
14. (2021九上·淮安月考) 已知在△ABC中，∠B＝45°，AB＝8 $\text{[math]}$ ，AC＝10，则BC＝.

答案解析收藏纠错 + 选题
15. (2024九上·潮州期末) 如图，正方形ABCD的边长为3，以A为圆心，AB的长为半径画弧，连接AC，以A为圆心，AC的长为半径画弧，交AD的延长线于点E，则图中阴影部分的面积是 .

答案解析收藏纠错 + 选题
16. (2021九上·淮安月考) 如图，在边长为 $\text{[math]}$ 的等边△ABC中，动点D，E分别在BC，AC边上，且保持AE＝CD，连接BE，AD，相交于点P，则CP的最小值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·淮安月考)
1. （1）计算： $\text{[math]}$ +|﹣1|﹣（ $\text{[math]}$ ）^﹣²﹣4sin60°；
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2021九上·淮安月考) 解不等式组： $\text{[math]}$ ，并求出所有整数解的和.

答案解析收藏纠错 + 选题
19. (2021九上·淮安月考) 如图，在 $\text{[math]}$ 中，点E是AB边中点，DE与CB的延长线交于点F.求证： DE=FE.

答案解析收藏纠错 + 选题
20. (2021九上·淮安月考) 某学校为了解学生上学的交通方式，现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查，规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项，并根据统计结果绘制成如下两幅不完整的统计图.
请解答下列问题：
1. （1）在这次调查中，样本容量为；
2. （2）补全条形统计图；
3. （3） “乘车”所对应的扇形圆心角为°；
4. （4）若该学校共有2000名学生，试估计该学校学生中选择“步行”方式的人数.
答案解析收藏纠错 + 选题
21. (2021九上·淮安月考) 4件同型号的产品中，有1件不合格品和3件合格品．
1. （1）从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；
2. （2）在这4件产品中加入 $\text{[math]}$ 件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验．通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出 $\text{[math]}$ 的值大约是多少．
答案解析收藏纠错 + 选题
22. (2021九上·淮安月考) 如图，在东西方向的海岸线上的两个码头 $\text{[math]}$ 和 $\text{[math]}$ 相距54海里，现有一货轮从码头 $\text{[math]}$ 出发沿正北方向航行9海里到达点 $\text{[math]}$ 处，测得灯塔 $\text{[math]}$ 在点 $\text{[math]}$ 的北偏西 $\text{[math]}$ 方向上，已知灯塔 $\text{[math]}$ 在码头 $\text{[math]}$ 的北偏东 $\text{[math]}$ 方向，求此时货轮与灯塔 $\text{[math]}$ 的距离.

答案解析收藏纠错 + 选题
23. (2021九上·淮安月考) 如图，在平面直角坐标系xOy中，直线l：y＝kx﹣1（k≠0）与函数y $\text{[math]}$ （x＞0）的图象交于点A（3，2）．
1. （1）求k，m的值；
2. （2）将直线l沿y轴向上平移t个单位后，与y轴交于点C，与函数y $\text{[math]}$ （x＞0）的图象交于点D．
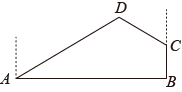
  ①当t＝2时，求线段CD的长；
  
  ②若 $\text{[math]}$ CD≤2 $\text{[math]}$ ，结合函数图象，直接写出t的取值范围．
答案解析收藏纠错 + 选题
24. (2021九上·淮安月考) 如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC.
1. （1）求证：DE是⊙O的切线.
2. （2）已知：BC＝8cm，AD＝3cm，求线段AE的长.
答案解析收藏纠错 + 选题
25. (2021九上·砀山期末) 端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：
小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克.

根据他们的对话，解决下面所给问题：
1. （1）超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？
2. （2）设该水果超市一天可获利润 $\text{[math]}$ 元.求当该商品每件售价为多少元时，该网店一天所获利润最大？并求最大利润值.
答案解析收藏纠错 + 选题
26. (2021九上·淮安月考) 我们曾经研究过：如图1，点P在⊙O外或点P在⊙O内，直线PO分别交⊙O于点A、B，则线段PA是点P到⊙O上各点的距离中最短的线段，线段PB是点P到⊙O上各点的距离中最长的线段.

（运用）在Rt△ABC中，∠BAC＝90°，AB＝AC＝2，点E是AC的中点.
1. （1）如图2，若F是BC边上一动点，将△CEF沿EF所在的直线翻折得到△C′EF，连接C′B，则C′B的最小值是
2. （2）如图3，若取AB的中点D，连接DE，得等腰Rt△ADE，将△ABC绕点A旋转，点P为射线BD，CE的交点，点Q是AE的中点.
  ①BD与CE的位置关系是 ▲
  
  ②连接PQ，求PQ的最大值和最小值.
3. （3）（拓展）喜欢研究的小聪把上述第（2）问图中的△ADE绕点A旋转，而△ABC不动，记点P为射线BD，CE的交点（如图4），他发现在旋转过程中线段PB的长度存在最值，请直接写出PB的最小值
答案解析收藏纠错 + 选题
27. (2021九上·淮安月考) 如图，二次函数y₁＝ax²+bx+c的图象与x轴交于点A（-1，0），B（3，0），与y轴交于点C（0，3）.
1. （1）直接写出二次函数的表达式；以及顶点D的坐标.
2. （2） ①若点P（0，t）（t<-1）是y轴上的点，将点Q（-5，0）绕着点P按照顺时针方向旋转90°得到点E，当点E恰好落在二次函数图象上时，求t的值；
  ②在①的条件下，连接AD、AE，设∠DAE=α，若点N是抛物线上动点，将射线CB绕点C旋转α角度后过点N，求N点的坐标.
3. （3）将二次函数y₁的图象沿x轴翻折得到y₂ ，设y₁与y₂组成的图形为M，直线L；y=-x+m与M有公共点，直接写出：L与M的公共点为3个时，m的值.
答案解析收藏纠错 + 选题