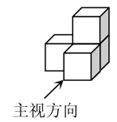
 B .
B .  C .
C .  D .
D . 
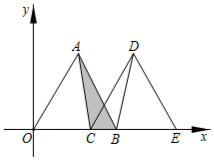
①若此函数的图象为直线,则此函数的图象和直线
平行;
②若此函数的图象为双曲线,则此函数的图象分布在第一、三象限;
③若此函数的图象为抛物线,且开口向下,则此函数图象一定与
轴的负半轴相交;
④若此函数的图象为抛物线,且开口向上,则此函数图象对称轴在直线
左侧。
所有合理推断的序号是( )
名学生的成绩(满分为100分)统计如下(单位:分): 90,74,88,65,98,75,81,44. 85,70,55,80,95,88,72,87,60,56,76,66,78,72,82,63,100
| 成绩
|
|
|
|
|
| 人数 |
______ |
10 |
8 |
______ |
分析数据:补充完成下面的统计分析表:
| 平均数 |
中位数 |
方差 |
| 76 |
______ |
190.88 |
②连接
、
、
.当
的度数为时,四边形
是菱形.
①求
关于
的关系式.
②进货时,
种礼品的购进数量不少于60个,已知
种礼品每个的售价为38元,
种礼品每个的售价为50元,若该店全部售完可获利
元,求
关于
的关系式,并说明应该如何进货才能使该店所获利润最大.

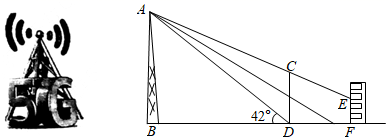
⑴小星分析发现,有三种可能存在的情况,其中,当
时,通过推理计算可得
的长为
.但当他进一步研究其余两种情况时,发现很难通过常规的推理计算得到
的长,于是尝试利用学习函数的经验解决问题.
⑵小星将线段
的长度记为
,
和
的长度分别记为
,
,并分别对函数
,
随着自变量
的变化规律进行探究.小星通过取点、画图、测量,得到了下表中的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
①在探究过程中,小星发现当
时,无须测量可以求出
的长,此时
的长约为
(结果精确到
.参考数据:
).
②利用表格中的数据,小星已经在图2所示的平面直角坐标系中画出了
关于
的函数图象,请你根据上文中
和
的
组对应值在此平面直角坐标系中描点,并画出
关于
的函数图象
⑶小星发现,想用函数图象彻底解决这个问题,还需要在平面直角坐标系内再画出一个函数的图象,请直接写出这个函数的解析式: , 并在上述平面直角坐标系中画出该函数的图象.
⑷请结合图象直接写出:当
是
或
的
倍时,
的长约为(结果精确到
).