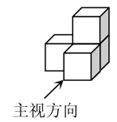
 B .
B .  C .
C .  D .
D . 


| 等级 | 次数 | 频率 |
| 不合格 | 100≤x | a |
| 合格 | 120≤x | b |
| 良好 | 140≤x | |
| 优秀 | 160≤x |
请结合上述信息完成下列问题:
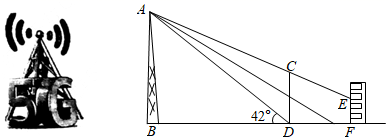
①求y关于x的关系式.
②进货时,A种礼品的购进数量不少于60个,已知A种礼品每个的售价为38元,B种礼品每个的售价为50元,若该店全部售完可获利W元,求W关于x的关系式,并说明应该如何进货才能使该店所获利润最大.
②连接、
、
. 当
的度数为时,四边形
是菱形.
①若 , 问
与
是否会全等?说明理由;
②线段把
分成两个三角形,若这两个三角形的面积比为
, 求出m的值.
①当时,试求
的值.
②在中,过点D作
于点E,延长至点H,
, 若
, 证明:
.