 B .
B .  C .
C .  D .
D . 


 B .
B .  C .
C .  D .
D . 

①月上网时间不足35小时,选择方式A最省钱;
②月上网时间超过55小时且不足80小时,选择方式C最省钱;
③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元;
④对于上网方式A,若月上网时间超出25小时,则超出的时间每分钟收费0.05元.
所有合理推断的序号是( )




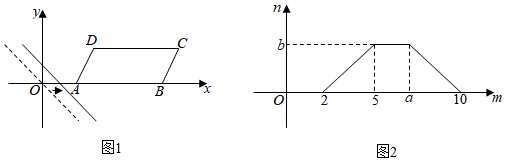
已知:如图,在Rt△ABC中,∠ABC=90°,O为AC的中点.

求作:四边形ABCD,使得四边形ABCD是矩形.
作法:①作射线BO,以点O为圆心,OB长为半径画弧,交射线BO于点D;
②连接AD,CD.
四边形ABCD是所求作的矩形.
根据小东设计的尺规作图过程,
证明:∵点O为AC的中点,
∴AO=CO.
又∵BO= ▲ ,
∴四边形ABCD是平行四边形( )(填推理的依据).
∵∠ABC=90°,
∴▱ABCD是矩形( )(填推理的依据).


收集数据
从A,B两个校区八年级各随机抽取20名学生,进行了垃圾分类有关知识测试,测试成绩(百分制)如下:
A校区 87 75 79 82 77 76 86 71 76 91
76 80 82 68 73 81 88 69 84 78
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 55 83
按如下表分数段整理、描述这两组样本数据:
|
成绩x人数 校区 |
50≤x≤59 |
60≤x≤69 |
70≤x≤79 |
80≤x≤89 |
90≤x≤100 |
|
A |
0 |
2 |
9 |
8 |
1 |
|
B |
|
|
7 |
|
2 |
(说明:成绩80分及以上为掌握程度优秀,70~79分为掌握程度良好,60~69分为掌握程度合格,60分以下为掌握程度不合格)
两组样本数据的平均数、中位数、众数如表所示:
|
校区 |
平均数 |
中位数 |
众数 |
|
A |
78.95 |
|
76 |
|
B |
78.75 |
80.5 |
|
得出结论
①估计B校区八年级对垃圾分类有关知识的掌握程度优秀的学生人数为 ;
②可以推断出校区的八年级学生对垃圾分类有关知识的掌握程度较好,理由为.(至少从两个不同的角度说明推断的合理性)

