山西省吕梁市交城县2022年中考模拟试卷（一）数学试题

更新时间：2024-07-13 浏览次数：100 类型：中考模拟

一、选择题

1. (2022·交城模拟) 下列各数中是无理数的是（）

A . 0 B . 1.21 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·交城模拟) 第二十四届冬季奥林匹克运动会于2022年2月20日在北京圆满落幕，中国体育健儿在本次运动会上取得了历史最好成绩，促进了全国冰雪运动的蓬勃发展．下面的图片都是冬奥会的会徽，上面有图案和文字说明，其中的图案是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·交城模拟) 1968年科学家发现世界上最小的物质是夸克，物质就是由这种极其小的物质而构成的，夸克有多小呢？它的大小是1介米，约为原子核的百万分之一．百万分之一用科学记数法表示为（）

A . 1×10^-5 B . 1×10^-6 C . 1×10⁶ D . 1×10^-8

答案解析收藏纠错 + 选题
4. (2022·交城模拟) 我国古代的数学家曾写下了许多数学名著，这些数学著作是了解古代数学成就的丰富宝库，其中有不少成就在世界范围内处于遥遥领先的地位.下列数学名著与其内容搭配不正确的一项是（）

A . 《周髀算经》勾股定理 B . 《九章算术》负数的概念和正负数的运算 C . 《海岛算经》三斜求积术 D . 《孙子算经》鸡兔同笼

答案解析收藏纠错 + 选题
5. (2022·交城模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·交城模拟) 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？如果译成白话文，其意思是：有100个和尚分100只馒头，正好分完.如果大和尚一人分3只，小和尚3人分一只，试问大、小和尚各有几人？设大和尚有 $\text{[math]}$ 人，则小和尚有（100－ $\text{[math]}$ ）人，根据题意列得方程（）

A . 3x+ $\text{[math]}$ =100 B . 3x+ $\text{[math]}$ （100－x）=100 C . $\text{[math]}$ +3（100－x）=100 D . $\text{[math]}$ x+（100－x）=100

答案解析收藏纠错 + 选题
7. (2022·交城模拟) 解分式方程 $\text{[math]}$ 时，去分母这一步方程两边不能同时乘以（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·交城模拟) 如图，在菱形ABCD中，∠ADC=120°，AB=4，连结AC，在AC上取一点F，使CF=CD，连结DF，则AF的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·交城模拟) 如图，正比例函数 $\text{[math]}$ 的图象经过点A（3，4），且与反比例函数 $\text{[math]}$ 的图象交于点B，C两点，点C是OA的中点，当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·交城模拟) 如图，正方形ABCD的边长是 $\text{[math]}$ ，以正方形对角线的一半OA为边作正六边形，其中一边与正方形的边CD交于点E，再以点O为圆心OE为半径画弧交AD于点F，则图中阴影部分的的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022·交城模拟) 用配方法把二次函数 $\text{[math]}$ 化成顶点式为．

答案解析收藏纠错 + 选题
12. (2022·交城模拟) 不等式组 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题
13. (2022·交城模拟) 在平面直角坐标系中，△ABC和△DEF是以原点O为位似中心的位似图形，其位似比为1：3，那么点A（1，3）的对应点D的坐标为．

答案解析收藏纠错 + 选题
14. (2022·交城模拟) 如图，平面直角坐标系中，点A（1，2）、点C（4，4）是矩形ABCD的两个顶点，AB与 $\text{[math]}$ 轴平行，则直线 $\text{[math]}$ 与矩形公共部分的线段EF长为．

答案解析收藏纠错 + 选题
15. (2022·交城模拟) 如图，把△ABC绕着点A逆时针旋转90°得到△ADE，连接BE，CD，M是BE的中点，若AM= $\text{[math]}$ ，则CD的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2022·交城模拟)
1. （1）计算： $\text{[math]}$ ÷sin45°．
2. （2）先化简，再求值： $\text{[math]}$ ，代入你喜欢的 $\text{[math]}$ ， $\text{[math]}$ 值求结果．
答案解析收藏纠错 + 选题
17. (2022·交城模拟) 我县某宾馆有若干间标准房，平时以市场管理部门批准的标价200元定价时（定价不得超过380元），平均每日可入住50间，在去年国庆黄金周中，为了增加营业额，该宾馆决定上调房价，经市场调查表明，定价每提高20元，每日入住房间数就减少1间，若不考虑其他因素，问国庆期间宾馆标准房的价格定为多少元时，每日的营业额可为11520元？

答案解析收藏纠错 + 选题
18. (2022·庐江模拟) 如图，△ABC内接于⊙O，AD与BC是⊙O的直径，延长线段AC至点G，使CG=AC，连接DG，点E在DG边上，并且∠ADG=2∠GCE．
1. （1）求证：CE是⊙O的切线；
2. （2）若AG=8，OA=5，求EG的长．
答案解析收藏纠错 + 选题
19. (2022·诸城模拟) 某校为了“中考体测”的顺利进行，引导同学们积极参加体育锻炼，学校购买了一批跳绳供学生借用，现从九年级随机抽取了部分学生对新跳绳进行测试，绘制了如下的两幅不完整的统计表和统计图．请根据相关信息，解答下列问题：
一分钟跳绳成绩的分组统计表
组别
跳绳次数分段
频数
A
$\text{[math]}$
10
B
$\text{[math]}$
$\text{[math]}$
C
$\text{[math]}$
42
D
$\text{[math]}$
13
一分钟跳绳成绩的扇形统计图
1. （1）本次接受随机抽样调查的学生人数为人，统计表中的 $\text{[math]}$ 的值为；
2. （2）抽取学生一分钟跳绳成绩的中位数所在的组别是；
3. （3）现在指定两名男生和两名女生负责跳绳发放和整理工作，若两人一组，随机组合，则恰好分组都是一男一女的概率是多少？
答案解析收藏纠错 + 选题
20. (2022·交城模拟) 阅读下列材料，并按要求完成相应的任务．
黄金三角形与五角星
当等腰三角形的顶角为36°（或108°）时，它的底与腰的比（或腰与底的比）为 $\text{[math]}$ ，我们把这样的三角形叫做黄金三角形．
按下面的步骤画一个五角星（如图）：
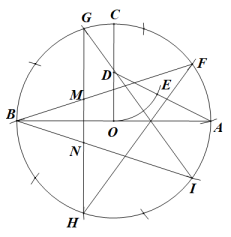
①作一个以AB为直径的圆，圆心为O；
②过圆心O作半径OC⊥AB；
③取OC的中点D，连接AD；
④以D为圆心OD为半径画弧交AD于点E；
⑤从点A开始以AE为半径顺时针依次画弧，
正好把⊙O十等分（其中点F，G，B，H，I为五等分点）；
⑥以点F，G，B，H，I为顶点画出五角星．
任务：
1. （1）求出 $\text{[math]}$ 的值为；
2. （2）如图，GH与BF，BI分别交于点M，N，求证：△BMN是黄金三角形．
答案解析收藏纠错 + 选题
21. (2022·交城模拟) 如图，是放在水平桌面上的台灯的几何图，已知台灯底座高度为2cm，固定支点O到水平桌面的距离为7.5cm，当支架OA、AB拉直时所形成的线段与点M共线且与底座垂直，此时测得B到底座的距离为31.64cm（线段AB，AO，OM的和），经调试发现，当∠OAB=115°，∠AOM=160°时，台灯所投射的光线最适合写作业，测量得A到B的水平距离为10cm，求此时点B到桌面的距离．（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
22. (2022·交城模拟) 综合与实践
问题情境

Rt△ABC和Rt△DEF如图1放置，点B与点D重合，∠ACB=∠EDF=90°，∠A=30°，AB=ED=FD=4，EF分别与AC，AB交于点N，点P，点M是AB的中点．
1. （1）数学思考
  连接MN，求证：点N是EF的中点；并计算△MNP的面积；
2. （2）操作探究
  如图2，先将△DEF沿BC的方向平移，使点D与点C重合，再沿CA的方向平移到点D为AC的中点时停止；过点C作CH∥AB交DE于点H，连接AH，AN，CM．试判断四边形AMCH的形状，并说明理由；
3. （3）在图2的基础上，将△DEF绕着点D顺时针旋转30°，CH∥AB仍然存在，延长CH交MN于点G，交EF于点Q，如图3．请直接写出三角形CMG的面积．
答案解析收藏纠错 + 选题
23. (2022·交城模拟) 如图1，已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于A（-1，0），B两点，与 $\text{[math]}$ 轴交于点C（0，-2）连接BC．
1. （1）求抛物线的解析式与直线BC的解析式；
2. （2）点P是直线BC下方抛物线上一动点（不与B，C重合），当PD⊥BC于点D时，求出PD的最大值，并求此时点P的坐标；
3. （3）如图2，连接AC，抛物线的对称轴为直线EF，点M是直线EF右侧抛物线上一点，连接AM交EF于点Q，过点M作MN⊥EF于点N，是否存在这样的点M，使得△QMN与△ACO相似？若存在，请直接写出点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题