重庆市江津区12校联盟学校2021-2022学年八年级下学期...

更新时间：2022-05-26 浏览次数：55 类型：期中考试

一、选择题：（本大题共12小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

1. (2022八下·江津期中) 二次根式 $\text{[math]}$ 中字母x的取值范围是（）

A . x=3 B . x>0 C . x≥3 D . x>-3

答案解析收藏纠错 + 选题
2. (2022八下·江津期中) 下列二次根式中属于最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022八下·江津期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ =-3 C . $\text{[math]}$ =-2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022八下·江津期中) 估计 $\text{[math]}$ 的值应在（）

A . 7和8之间 B . 8和9之间 C . 9和10之间 D . 10和11之间

答案解析收藏纠错 + 选题
5. (2022八下·江津期中) 以下列各组线段为边长，不能构成直角三角形的是（）

A . 6，8，10 B . 2，3，4 C . 1，5， $\text{[math]}$ D . 2，2， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八下·江津期中) 如图，点P是以A为圆心，AB为半径的圆弧与数轴的交点，则数轴上点P表示的实数是（）

A . -2 B . -2.2 C . $\text{[math]}$ D . 1- $\text{[math]}$

答案解析收藏纠错 + 选题
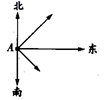
7. (2022八下·江津期中) 如图，一客轮以16海里/时的速度从港口A出发向东北方向航行，另一客轮同时以12海里/时的速度从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）

A . 25海里 B . 30海里 C . 35海里 D . 40海里

答案解析收藏纠错 + 选题
8. (2022八下·江津期中) 下面关于平行四边形的说法中，不正确的是（）

A . 对角线互相平分的四边形是平行四边形 B . 有一组对边平行，另一组对边相等的四边形是平行四边形 C . 两组对边分别相等的四边形是平行四边形 D . 有两组对角相等的四边形是平行四边形

答案解析收藏纠错 + 选题
9. (2022八下·江津期中)
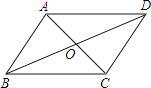
如图，▱ABCD的对角线AC，BD交于点O，已知AD=8，BD=12，AC=6，则△OBC的周长为（　　）

A . 13 B . 17 C . 20 D . 26

答案解析收藏纠错 + 选题
10. (2022八下·江津期中) 如图，一圆柱高8cm，底面半径为 $\text{[math]}$ cm，一只蚂蚁从点A沿圆柱侧面爬到点B处吃食，要爬行的最短路程是（）

A . 6cm B . 8cm C . 10cm D . 12cm

答案解析收藏纠错 + 选题
11. (2022八下·江津期中) 如图，四边形ABCD是平行四边形，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA．如果AD=5cm，AP=8cm，则△ABP的面积等于（）cm² ．

A . 24 B . 30 C . 6 $\text{[math]}$ D . 12 $\text{[math]}$

答案解析收藏纠错 + 选题

12. (2022八下·江津期中) 将从1开始的一组数按如图的规律排列：规定位于第m行第n列是的数记为（m，n）例如 $\text{[math]}$ 记为（4，2），按此规律， $\text{[math]}$ 记为（）

	第1列	第2列	第3列	第4列
第1行	1	$\text{[math]}$	$\text{[math]}$	2
第2行	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
第3行	3	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
第4行	4	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
……	……	……	……	……

A . （506，2） B . （506，3） C . （505，2） D . （505，3）

答案解析收藏纠错 + 选题

二、填空题：（本大题共4小题，每小题4分，共16分）将每小题的答案直接填写在答题卡中对应的横线上．

13. (2022八下·江津期中) 计算： $\text{[math]}$ =

答案解析收藏纠错 + 选题
14. (2022八下·江津期中) 如图，在 $\text{[math]}$ ABCD中，AE⊥BC于E，AC=AD，∠CAE=56°，则∠D= ．

答案解析收藏纠错 + 选题
15. (2022八下·江津期中) 如图，分别以等腰Rt△ACD的边AD，AC，CD为直径画半圆，AD=2，则阴影部分的面积是

答案解析收藏纠错 + 选题
16. (2022八下·江津期中) 如图，折叠直角三角形纸片ABC，使得两个锐角顶点A、C重合，设折痕为DE。若AB=4，BC=3，则△ADC的周长是

答案解析收藏纠错 + 选题

三、解答题（每小题8分，共16分）请将解答过程书写在答题卡中对应的位置上．

17. (2022八下·江津期中) 计算
1. （1）（-2）²+ $\text{[math]}$ × $\text{[math]}$ +（-6）⁰
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2022八下·江津期中) 如图，在 $\text{[math]}$ ABCD中，AB>BC．BE平分∠ABC
1. （1）尺规作图：作∠BAD的平分线交CD于点F．（保留作图痕迹，不写作法，不写结论）
2. （2）在（1）所作的图形中，BE与AF交于点P，求证：△ABP为直角三角形
答案解析收藏纠错 + 选题

四、解答题（每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

19. (2024八上·洪江期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 满足 $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2022八下·江津期中) 如图，在△ABC中，CD⊥AB于点D，AC=4，BC=3，DB= $\text{[math]}$
1. （1）分别求出DC，AB的长；
2. （2）猜想：△ABC是什么特殊三角形，并证明你的猜想。
答案解析收藏纠错 + 选题
21. (2022八下·江津期中)
如图，▱ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N．
1. （1）求证：四边形CMAN是平行四边形．
2. （2）已知DE=4，FN=3，求BN的长．
答案解析收藏纠错 + 选题
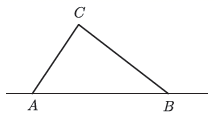
22. (2024八下·防城月考) 台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向 $\text{[math]}$ 由 $\text{[math]}$ 行驶向 $\text{[math]}$ ，已知点 $\text{[math]}$ 为一海港，且点 $\text{[math]}$ 与直线 $\text{[math]}$ 上的两点 $\text{[math]}$ ， $\text{[math]}$ 的距离分别为 $\text{[math]}$ ， $\text{[math]}$ ，又 $\text{[math]}$ ，以台风中心为圆心周围 $\text{[math]}$ 以内为受影响区域．
1. （1）求 $\text{[math]}$ 的度数．
2. （2）海港 $\text{[math]}$ 受台风影响吗？为什么？
3. （3）若台风的速度为20千米/小时，当台风运动到点 $\text{[math]}$ 处时，海港 $\text{[math]}$ 刚好受到影响，当台风运动到点 $\text{[math]}$ 时，海港 $\text{[math]}$ 刚好不受影响，即 $\text{[math]}$ ，则台风影响该海港持续的时间有多长？
答案解析收藏纠错 + 选题
23. (2022八下·江津期中) 在数学课外学习活动中，小明和他的同学遇到一道题：
已知a= $\text{[math]}$ ，求2a²-8a+1的值．他是这样解答的：

∵a= $\text{[math]}$

∴a-2= $\text{[math]}$

∵（a-2）²=3，a²-4a+4=3．

∴a²-4a=-1．

∴2a²-8a+1=2（a²-4a）+1=2×（-1）+1=-1．

请你根据小明的解题过程，解决如下问题：
1. （1） $\text{[math]}$ =
2. （2）化简 $\text{[math]}$
3. （3）若a= $\text{[math]}$ ，求a⁴-4a³-4a+4的值．
答案解析收藏纠错 + 选题
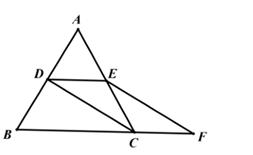
24. (2022八下·江津期中) 如图，在△ABC中，AB=AC=4，D，E分别为AB，AC的中点，连接CD，过点E作EF∥DC交BC的延长线于点F。
1. （1）求证：DE=CF
2. （2）若∠B=60°，求EF的长
答案解析收藏纠错 + 选题
25. (2022八下·江津期中) 如图，在平面直角坐标系中有三点A（3，0），B（0，4），C（2，5）。
1. （1）求A，B两点之间的距离；
2. （2）求△ABC的面积。
3. （3）在x轴上有一点D，使△ABD为等腰三角形，直接写出点D的坐标。
答案解析收藏纠错 + 选题