2022年北师大版初中数学七年级下学期期中模拟试题4

① ；② ；③ ；④ .

则当 时，所捂多项式的值是

有如下四个结论：

①（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵；

②当a=-2，b=1时，代数式a³+3a²b+3ab²+b³的值是-1；

③当代数式a⁴+4a³b+6a²b²+4ab³+b⁴的值是0时，一定是a=-1，b=1；

④（a+b）ⁿ的展开式中的各项系数之和为2n．

上述结论中，正确的有（写出序号即可）．

①先化简，再求值： (a²b-2ab²-b³)÷b-(a-b)(a+b)，其中a=-2， .

②若x²+ax+8和多项式x²-3x+b相乘的积中不含x³、x²项，求ab的值.

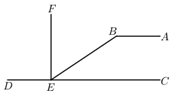
如图，点B在AG上，AGCD，CF平分∠BCD，∠ABE＝∠FCB，BE⊥AF点E．

求证：∠F＝90°．

证明：∵AGCD（已知）

∴∠ABC＝∠BCD（                  ▲                  ）

∵∠ABE＝∠FCB（已知）

∴∠ABC﹣∠ABE＝∠BCD﹣∠FCB

即∠EBC＝∠FCD

∵CF平分∠BCD（已知）

∴∠BCF＝∠FCD（                  ▲                  ）

∴                  ▲                  ＝∠BCF（等量代换）

∴BECF（                  ▲                  ）

∴                  ▲                  ＝∠F（                  ▲                  ）

∵BE⊥AF（已知）

∴                  ▲                  ＝90°（                  ▲                  ）

∴∠F＝90°．

如图，它表示甲乙两人从同一个地点出发后的情况．到十点时，甲大约走了13千米．根据图象回答：

（1）甲是几点钟出发？

（2）乙是几点钟出发，到十点时，他大约走了多少千米？

（3）到十点为止，哪个人的速度快？

（4）两人最终在几点钟相遇？

（5）你能利用图象中得到的信息，编个故事吗？