 B .
B .  C .
C .  D .
D . 
属于确定事件的有( )




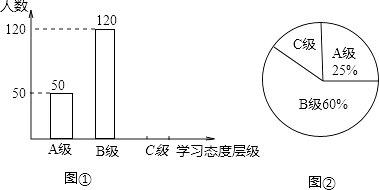
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 127 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.254 | 0.254 | a |
每天课外阅读时间t/h | 频数 | 频率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合计 | a | 1 |
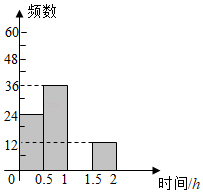
根据以上信息,回答下列问题:
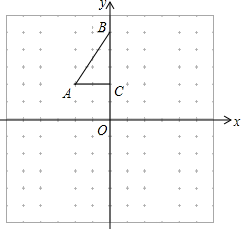
⑴画 , 使它与
关于点
成中心对称;
⑵平移 , 使点
的对应点
坐标为(-2,-6),画出平移后对应的
;
⑶若将绕某一点旋转可得到
, 则旋转中心的坐标为____.


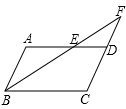
【发现与证明】在ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.


将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2 ,CE=2,求线段AE的长.