【整理数据】
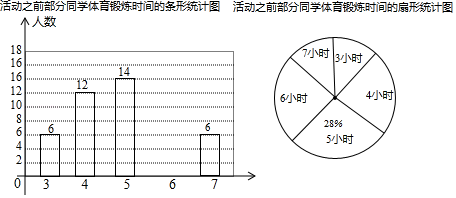
“爱生活•爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
| 一周体育锻炼时间(小时) | 3 | 4 | 5 | 6 | 7 |
| 人数 | 3 | 5 | 15 | a | 10 |
活动之后部分学生体育锻炼时间的统计表
【分析数据】
| 平均数 | 中位数 | 众数 | |
| 活动之前锻炼时间(小时) | 5 | 5 | 5 |
| 活动之后锻炼时间(小时) | 5.52 | b | c |
请根据调查信息分析:
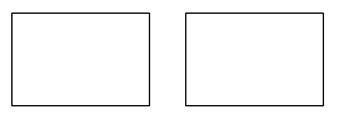
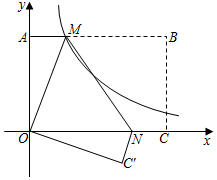
已知某矩形长为8,宽为6,请你用虚线在下图中分别画出两种不同折法的菱形的示意图
并在下方横线上直接写出菱形的面积(画图特别说明: ①示意图中体现所有折痕;②菱形的顶点必须都在矩形的边上 ;③所画菱形是能仅用已知数据便可求出面积的图形)
A、B两种型号车的进货和销售价格如表:
|
A型车 |
B型车 |
|
|
进货价格(元) |
1200 |
1400 |
|
销售价格(元) |
今年的销售价格 |
2200 |