
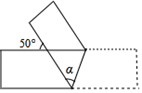
 B .
B .  C .
C .  D .
D . 


证明:∵AB∥CD(已知)
∴∠B=∠ ▲ (两直线平行,内错角相等)
∵∠B=∠D(已知)
∴∠D=∠ ▲ ( )
∴ED// ▲ ( )
∴∠E=∠BCA( )


①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180° ▲
∵AB∥CD,EF∥AB,
∴ ▲ ∥ ▲ , (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+ ▲ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.
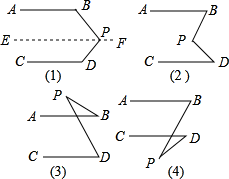
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.