 B .
B .  C .
C .  D .
D . 
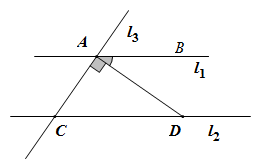


 B .
B .  C .
C .  D .
D . 


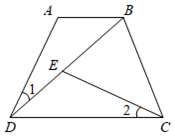
|
主题 |
频数 |
频率 |
|
A党史 |
6 |
0.12 |
|
B新中国史 |
20 |
m |
|
C改革开放史 |
0.18 |
|
|
D社会主义发展史 |
15 |
n |
|
合计 |
50 |
1 |

请结合上述信息完成下列问题:
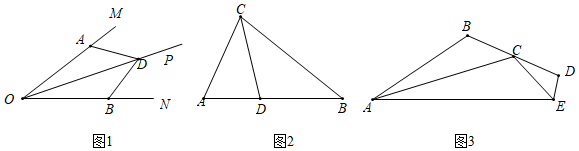
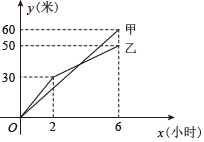
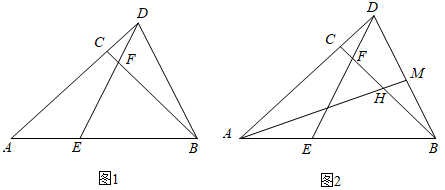
①求线段AD的值;
②设AH=a,用含a的代数式表示线段BM的值.