浙江省绍兴市上虞区2022年初中毕业生学业评价文化考试适应性...

更新时间：2022-05-26 浏览次数：270 类型：中考模拟

一、选择题（本大题有10小题，每小题4分，共40分．请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分）

1. (2022·上虞模拟) 实数2，0，-2， $\text{[math]}$ 中，最大的数是（）

A . 2 B . 0 C . -2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·上虞模拟) 我国历来实行耕地保护党政同责，落实“长牙齿”的耕地保护硬措施，严守1800000000亩耕地红线．这个数字00000000用科学记数法可表示为（）

A . 0.18×10¹⁰ B . 1.8×10¹⁰ C . 18×10⁸ D . 1.8×10⁹

答案解析收藏纠错 + 选题
3. (2022·上虞模拟) 如图，将七巧板的其中几块拼成一个多边形，所拼多边形为轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·龙湾模拟) 如图的几何体由五个相同的小正方体搭成，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022·上虞模拟) 如图，在平面直角坐标系中，点（2，2）是一个光源，木杆AB两端的坐标分别为（0，1），（3，1）．则木杆AB在x轴上的投影AB长为（）

A . 2 $\text{[math]}$ B . 3 $\text{[math]}$ C . 5 D . 6

答案解析收藏纠错 + 选题
6. (2022·上虞模拟) 在一个不透明的袋中装有6个只有颜色不同的球，其中2个红球、1个黄球和3个白球，从袋中任意摸出一个球，是白球的概率为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·上虞模拟) 如图，四边形ABCD为⊙O的内接四边形，已知∠BCD=120°，则∠BOD的度数为（）

A . 100° B . 110° C . 120° D . 130°

答案解析收藏纠错 + 选题
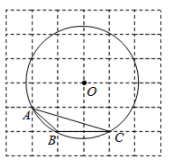
8. (2022·上虞模拟) 如图，在6×6的正方形网格中，每个小正方形的边长都是1，点A，B，C均在网格交点上，⊙O是△ABC的外接圆，则sin∠BAC的值为（）

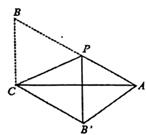
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·上虞模拟) 如图，在Rt△ABC中，∠C=90°，∠A=30°，BC= $\text{[math]}$ ，点P是斜边AB上一动点连结CP，将△BCP以直线CP为对称轴进行轴对称变换，B点的对称点为B'，连结AB'，则在P点从点A出发向点B运动的整个过程中，线段AB'长度的最小值为（）．

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ -1 D . 3- $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·上虞模拟) 一次函数y= kx+b的图象过点P （2，8），且分别与x轴和y轴的正半轴交于A，B两点，点O为坐标原点．当△AOB面积最小时，则k+b的值为（）

A . 10 B . 12 C . 14 D . 16

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题5分，共30分．）

11. (2022·上虞模拟) 分解因式：9-x²=．

答案解析收藏纠错 + 选题
12. (2022·上虞模拟) 不等式3（1-x）>2（1-2x）的解是．

答案解析收藏纠错 + 选题
13. (2022·上虞模拟) 我国古代数学名著《孙子算经》上有这样一道题：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？若设鸡x只，兔y只，则由头数可列出方程x+ y = 35，那么由足数可列出的方程为

答案解析收藏纠错 + 选题
14. (2022·上虞模拟) 在△ABC中，AB=AC，∠BAC=40°，D为BC边的中点，以点D为圆心，DA长为半径作弧，交直线BC于点P，连结AP．则∠BAP的度数是

答案解析收藏纠错 + 选题
15. (2022·上虞模拟) 如图，在平面直角坐标系中，一次函数y=-2x +4的图象与两坐标轴的正半轴分别交于点A，B，以AB为三角形一边作等边△ABC，顶点C在反比例函数y= $\text{[math]}$ 的图象上，则k=

答案解析收藏纠错 + 选题
16. (2022·上虞模拟) 在Rt△ABC中，∠C=90°，BC=3，AC=4，D是射线AB上的一个动点，点E与点A关于直线CD对称，当AD=时，△ADE为直角三角形．

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程．）

17. (2022·上虞模拟)
1. （1）计算： $\text{[math]}$ -6sin60°+ （1-π）⁰ ．
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2022·上虞模拟) 杭州2022年第19届亚运会，绍兴市将承办篮球、排球、棒球、垒球、黎岩5个项目的比赛．为了解学生对这些比赛项目的喜欢程度，某校随机抽查了部分学生进行问卷调查，要求每名学生只选其中最喜欢的一个项目，并将抽查结果绘制成如下不完整的统计图．

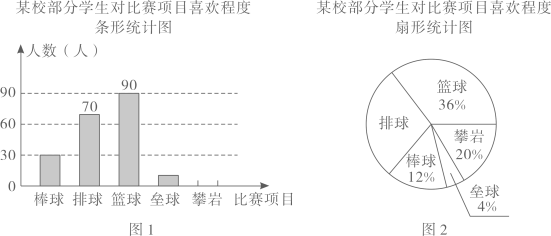
根据图中信息，解答下列问题：
1. （1）本次接受问卷调查的学生有多少人？在图1中补全条形统计图并求图2中“攀岩”的扇形圆心角的度数．
2. （2）全校共有1500名学生，请你估计全校学生中最喜欢“篮球”或“排球”的学生，各有多少人．
答案解析收藏纠错 + 选题
19. (2022·上虞模拟) 绍兴首条智慧快速路于今年3月19日正式通车．该快速路上M，N两站相距20km，甲、乙两名杭州亚运会会务工作志愿者从M站出发前往N站附近的比赛场馆开展服务．甲乘坐无人驾驶小巴，乙乘坐无人驾驶汽车．图中OC，AB分别表示甲、乙离开M站的路程s（km）与时间t（min）的函数关系的图象．
根据图象解答下列问题：
1. （1）填空：甲比乙提前分钟出发；无人驾驶小巴的速度为km/min；当乙乘坐无人驾驶汽车到达N站时，无人驾驶小巴离N站还有km．
2. （2）求乙离开M站的路程s（km）与时间t（min）的函数关系式并说明图中两函数图象交点P的实际意义．
答案解析收藏纠错 + 选题
20. (2022·上虞模拟) 如图，已知O是矩形ABCD对角线的交点，AD=2，AB=4，作DE∥AC，CE∥BD，DE，CE交于点E．
1. （1）记∠ECD=α，求sinα的值．
2. （2）求四边形EDOC的周长与面积．
答案解析收藏纠错 + 选题
21. (2022·上虞模拟) 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的“飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有二次函数关系．小明在一次击球过程中测得一些数据，如下表所示．
根据相关信息解答下列问题．

飞行时间t/s

0

1

2

飞行高度h/m

0

15

20
1. （1）求小球的飞行高度h（单位：m）关于飞行时间t（单位：s）的二次函数关系式．
2. （2）小球从飞出到落地要用多少时间？
3. （3）小球的飞行高度能否达到20.5m？如果能，请求出相应的飞行时间；如果不能，请说明理由．
答案解析收藏纠错 + 选题
22. (2022·上虞模拟) 如图，海岸线上有两座灯塔A，B，灯塔A位于灯塔B的正东方向，与灯塔B相距8km．海上有甲、乙两艘货船，甲船位于灯塔B的北偏东30°方向，与灯塔B相距8km的C处；乙船位于灯塔A的北偏东15°方向，与灯塔A相距6 $\text{[math]}$ km的D处．求：
1. （1）甲船与灯塔A之间的距离．
2. （2）两艘货船之间的距离．
答案解析收藏纠错 + 选题
23. (2022·上虞模拟) 正方形ABCD中，点E，F'分别在边BC，CD上，且AE平分∠BAF．
1. （1）如图1，若点E是BC的中点，求 $\text{[math]}$ 的值．
2. （2）如图2，若点F是CD的中点，求 $\text{[math]}$ 的值．
3. （3）如图3，若去掉条件“AE平分∠BAF”，增加条件“BE=2EC，∠EAF=30°”，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2022·上虞模拟) 如图1，在Rt△ABC中，∠B=90°，B=2AB=4，点D，E分别是边BC，AC的中点，连结DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
1. （1）通过画图探究，发现：．
  ①当α=0°时， $\text{[math]}$ =；②当α=180°时， $\text{[math]}$ =.
2. （2）当0°≤α<360°时，试判断 $\text{[math]}$ 是否是定值？请仅就图2所示情形给出证明．
3. （3）当△EDC旋转至A，D，E三点共线时：
  ①求线段BD的长；
  ②设P为射线BD上的一动点，若以PC，E三点为顶点的三角形是直角三角形，试求BP的长．（直接写出答案即可）
答案解析收藏纠错 + 选题