浙江省宁波市江北区2022年九年级中考数学模拟试卷（二模）

更新时间：2024-07-13 浏览次数：242 类型：中考模拟

一、单选题

1. (2022·浑南模拟) -3的相反数是（）

A . $\text{[math]}$ B . -3 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八下·青岛期末) 下列图形是用数学家的名字命名的，其中既是轴对称图形又是中心对称图形的是（）

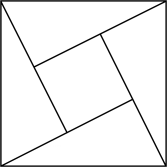
A . 赵爽弦图 B . 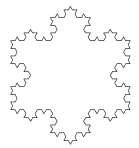科勒曲线 C . 笛卡尔心形曲线 D . 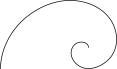斐波那契螺旋曲线

答案解析收藏纠错 + 选题
3. (2022·江北模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·江北模拟) 神舟号载人飞船于2021年10月16日凌晨成功对接中国空间站，自升空以来神舟十三号飞船每天绕地球16圈，按地球赤道周长计算神舟十三号飞船每天飞行约641200千米，641200用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·江北模拟) 如图所示的几何体是由一个圆锥和一个圆柱组成的，它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题

6. (2022·江北模拟) 甲、乙、丙、丁四地去年同期的平均气温 $\text{[math]}$ （单位： $\text{[math]}$ ）和方差 $\text{[math]}$ （单位： $\text{[math]}$ ）如下表．根据表中数据，要从中选取一处气温低且稳定的地区举办高山滑雪比赛，应选择（）

	甲	乙	丙	丁
$\text{[math]}$	-2	-2	0	-1
$\text{[math]}$	3	0.8	1.6	0.8

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

7. (2022·江北模拟) 无论 $\text{[math]}$ 取什么数，总有意义的代数式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七下·新田期末) 我国古代数学名著《算法统宗》中记载：“今有绫七尺，罗九尺，共价适等；只云罗每尺价比绫每尺少钱三十六文，问各钱价若干? ” 意思是：现在有一匹7尺长的绫布和一匹9 尺长的罗布恰好一样贵，只知道每尺罗布比绫布便宜36文，问两种布每尺各多少钱? 设绫布每尺 $\text{[math]}$ 文，罗布每尺 $\text{[math]}$ 文，那么可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·江北模拟) 抛物线 $\text{[math]}$ 经过（-2，m），（1，m）两点，若点A（x₁ ， y₁），B（x₂ ， y₂），也在抛物线上，且满足 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
10. (2022·江北模拟) 如图，以Rt $\text{[math]}$ 的各边为边分别向外作正方形， $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，若要求出 $\text{[math]}$ 的面积，只需知道（）

A . $\text{[math]}$ 的面积 B . 正方形 $\text{[math]}$ 的面积 C . 正方形 $\text{[math]}$ 的面积 D . 正方形 $\text{[math]}$ 的面积

答案解析收藏纠错 + 选题

二、填空题

11. (2022·义乌期中) $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2024九上·浔阳月考) 分解因式： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
13. (2022·江北模拟) 某路口红绿灯的时间设置为：红灯30秒，绿灯27秒，黄灯3秒．当人或车随意经过该路口时，遇到红灯的概率是．

答案解析收藏纠错 + 选题
14. (2022·江北模拟) 如图，在⊙O中，AE是直径，半径OC垂直于弦AB于D，连接BE，若AB=2 $\text{[math]}$ ，CD=1，则BE的长是.

答案解析收藏纠错 + 选题
15. (2022·江北模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 延长线上一点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值是．

答案解析收藏纠错 + 选题
16. (2022·江北模拟) 如图，点 $\text{[math]}$ 是菱形的四个顶点，其中点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，且点 $\text{[math]}$ 关于原点成中心对称，点 $\text{[math]}$ 的横坐标相等，则 $\text{[math]}$ 的值为；过点 $\text{[math]}$ 作AE// $\text{[math]}$ 轴交反比例函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，连结 $\text{[math]}$ 并延长交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连结 $\text{[math]}$ ．若S_△DOF=7，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·江北模拟)
1. （1）化简： $\text{[math]}$ ．
2. （2）解不等式组： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2022·双辽模拟) 第24届冬奥会于2022年2月在北京举行，为推广冰雪运动，发挥冰雪项目的育人功能，教育部近年启动了全国冰雪运动特色学校的䢯选工作．某中学通过将冰雪运动 “早地化” 的方式积极开展了基础滑冰、早地滑雪、早地冰球、早地冰显四个运动项目，要求每一位学生都自主选择一个运动项目，为了了解学生选择冰雪运动项目的情况，随机抽取了部分学生进行调查，并根据调查结果绘制成如下不完整的条形统计图和扇形统计图．
1. （1）这次随机抽取了 ▲ 名学生进行调查，并将条形统计图补充完整．
2. （2）求扇形统计图中 “旱地冰壶” 部分的圆心角度数．
3. （3）如果该校共有2400名学生，请你估计全校学生中喜欢基础滑冰项目有多少人?
答案解析收藏纠错 + 选题
19. (2022·江北模拟) 图1，图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图，已知运动员的小腿 $\text{[math]}$ 与斜坡 $\text{[math]}$ 垂直，大腿 $\text{[math]}$ 与斜坡 $\text{[math]}$ 平行，且 $\text{[math]}$ 三点共线，若雪仗 $\text{[math]}$ 长为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求此刻运动员头部 $\text{[math]}$ 到斜坡 $\text{[math]}$ 的高度 $\text{[math]}$ （精确到 $\text{[math]}$ ）（参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2022·江北模拟) 如图1、图2、图3 均是 $\text{[math]}$ 的正方形网格，每个小正方形边长为1，点 $\text{[math]}$ 、 $\text{[math]}$ 均在格点上.只用无刻度的直尺，分别按照下列要求画图．
1. （1）在图1中画一个 $\text{[math]}$ ，使得 $\text{[math]}$ ，且点 $\text{[math]}$ 在格点上．
2. （2）在图2中，画出线段 $\text{[math]}$ 的垂直平分线．
3. （3）在图3中，画一个四边形 $\text{[math]}$ ，使得 $\text{[math]}$ ，且点 $\text{[math]}$ 均在格点上．
答案解析收藏纠错 + 选题
21. (2022·江北模拟) 如图，已知二次函数 $\text{[math]}$ 图象的顶点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，与直线 $\text{[math]}$ 相交于O、B两点，点O是原点．
1. （1）求二次函数的解析式；
2. （2）求点 $\text{[math]}$ 的坐标；
3. （3）直接写出不等式 $\text{[math]}$ 的解．
答案解析收藏纠错 + 选题

22. (2022·江北模拟) 如图1 ，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，连结 $\text{[math]}$ ．设 $\text{[math]}$ $\text{[math]}$ ，小宁根据学习函数的经验，对变量 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系进行了如下探究．

（1）【探究】列表：通过观察补全下表（精确到 0.01）．

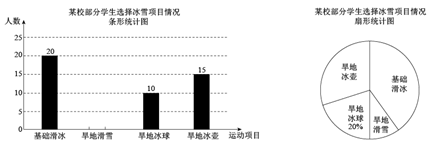
$\text{[math]}$	15	30	45	60	75	90	105	120	135	150	165
$\text{[math]}$	1.72		1.08		0.37	0		0.73	1.08	1.41	1.72

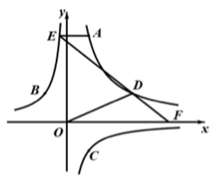
描点、连线：在图2中描出表中各组数值所对应的点 $\text{[math]}$ ，并画出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数图象．

（2）【发现】结合画出的函数图象，写出该函数的两条性质：
①；

②．
（3）【应用】有一种 “千斤顶”，它是由4根长为 $\text{[math]}$ 的连杆组成的菱形 $\text{[math]}$ ，当手柄顺时针旋转时， $\text{[math]}$ 两点的距离变小（如图 3）．在这个过程中，当 $\text{[math]}$ 时， $\text{[math]}$ 的度数约为．（精确到1°）．

答案解析收藏纠错 + 选题

23. (2022·江北模拟) 项目化学习：车轮的形状．
【问题提出】车轮为什么要做成圆形，这里面有什么数学原理?
1. （1）
  【合作探究】
  
  探究 $\text{[math]}$ 组：如图1，圆形车轮半径为 $\text{[math]}$ ，其车轮轴心 $\text{[math]}$ 到地面的距离始终为 $\text{[math]}$ ．
  探究 $\text{[math]}$ 组：如图2，正方形车轮的轴心为 $\text{[math]}$ ，若正方形的边长为 $\text{[math]}$ ，求车轮轴心 $\text{[math]}$ 最高点与最低点的高度差．
  探究 $\text{[math]}$ 组：如图3，有一个破损的圆形车轮，半径为 $\text{[math]}$ ，破损部分是一个弓形，其所对圆心角为 $\text{[math]}$ ，其车轮轴心为 $\text{[math]}$ ，让车轮在地上无滑动地滚动一周，求点 $\text{[math]}$ 经过的路程．
  
  探究发现：车辆的平稳关键看车轮轴心是否稳定．
2. （2）
  【拓展延伸】如图4，分别以正三角形的三个顶点 $\text{[math]}$ 为圆心，以正三角形的边长为半径作 $\text{[math]}$ 圆弧，这个曲线图形叫做“莱洛三角形”．
  
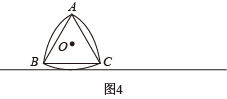
  探究 $\text{[math]}$ 组：使 “莱洛三角形” 沿水平方向向右滚动，在滚动过程中，其每时每刻都有 “最高点”，“中心点” 也在不断移动位置，那么在 “莱洛三角形” 滚动一周的过程中，其“最高点”和“中心点”所形成的图案大致是．
  延伸发现：“莱洛三角形”在滚动时始终位于一组平行线之间，因此放在其上的物体也能够保持平衡，但其车轴中心 $\text{[math]}$ 并不稳定．
答案解析收藏纠错 + 选题
24. (2022·江北模拟) 如图1，四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接四边形，其中 $\text{[math]}$ ，对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，在 $\text{[math]}$ 上取一点 $\text{[math]}$ ，使得 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）证明： $\text{[math]}$ ；
2. （2）如图 2，若 $\text{[math]}$ ，且 $\text{[math]}$ 恰好经过圆心 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）若 $\text{[math]}$ ，设 $\text{[math]}$ 的长为 $\text{[math]}$ ．
  ①如图3，用含有 $\text{[math]}$ 的代数式表示 $\text{[math]}$ 的周长；
  
  ②如图4， $\text{[math]}$ 恰好经过圆心 $\text{[math]}$ ，求 $\text{[math]}$ 内切圆半径与外接圆半径的比值．
答案解析收藏纠错 + 选题