山东省日照市五莲县2022年九年级中考一模考试数学试题

更新时间：2022-06-10 浏览次数：37 类型：中考模拟

一、单选题

1. (2022·罗山模拟) $\text{[math]}$ 的绝对值是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·杭州模拟) 下列运算一定正确的是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·五莲模拟) 2019年“五一”假日期间，某省银联网络交易总金额接近161亿元，其中161亿用科学记数法表示为（）

A . 1.61×10⁹ B . 1.61×10¹⁰ C . 1.61×10¹¹ D . 1.61×10¹²

答案解析收藏纠错 + 选题
4. (2023·广饶模拟) 如图是由10个同样大小的小正方体摆成的几何体．将小正方体①移走后，则关于新几何体的三视图描述正确的是（）

A . 俯视图不变，左视图不变 B . 主视图改变，左视图改变 C . 俯视图不变，主视图不变 D . 主视图改变，俯视图改变

答案解析收藏纠错 + 选题
5. (2022·五莲模拟) 如图，菱形ABCD的边AB=20，面积为320，∠BAD˂90°，⊙O的半径长等于（）

A . 5 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·五莲模拟) 已知 $\text{[math]}$ ，那么化简代数式 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . －3 D . 3

答案解析收藏纠错 + 选题
7. (2024九下·射洪模拟) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个实数根的平方和为12，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·五莲模拟) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ （ $\text{[math]}$ 为常数且 $\text{[math]}$ ）的图象都经过 $\text{[math]}$ ，结合图象，则不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·五莲模拟) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为直径， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 8 B . 10 C . 12 D . 16

答案解析收藏纠错 + 选题
10. (2024九上·道里开学考) 某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（）．

A . 20% B . 40% C . 18% D . 36%

答案解析收藏纠错 + 选题
11. (2022·五莲模拟) 如图，放置在直线l上的扇形OAB．由图①滚动（无滑动）到图②，再由图②滚动到图③．若半径OA＝2，∠AOB＝45°，则点O所经过的最短路径的长是（）

A . 2π+2 B . 3π C . $\text{[math]}$ D . $\text{[math]}$ +2

答案解析收藏纠错 + 选题
12. (2022·五莲模拟) 如图是二次函数 $\text{[math]}$ 的图像如图所示，图像过点（-3，0），对称轴在-1和-2之间，给出四个结论：① $\text{[math]}$ ② $\text{[math]}$ ③ $\text{[math]}$ ④ $\text{[math]}$ ．其中正确的结论是（）

A . ②④ B . ①④ C . ②③ D . ①③

答案解析收藏纠错 + 选题

二、填空题

13. (2022·五莲模拟) 因式分解： $\text{[math]}$ =

答案解析收藏纠错 + 选题
14. (2022·五莲模拟) 如图，Rt△AOB中，∠AOB＝90°，顶点 $\text{[math]}$ ， $\text{[math]}$ 分别在反比例函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象上，则tan∠BAO的值为．

答案解析收藏纠错 + 选题
15. (2022·东营模拟) 如图，小明在距离地面30米的P处测得A处的俯角为15°，B处的俯角为60°．若斜面坡度为1： $\text{[math]}$ ，则斜坡AB的长是米．

答案解析收藏纠错 + 选题
16. (2022·五莲模拟) 将被3整除余数为1的正整数，按照下列规律排成一个三角形数阵，则第20行第19个数是．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·五莲模拟) 计算
1. （1） $\text{[math]}$
2. （2）先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2022·五莲模拟) 某体育老师统计了七年级甲、乙两个班女生的身高，并绘制了以下不完整的统计图．

请根据图中信息，解决下列问题：
1. （1）两个班共有女生多少人？
2. （2）将频数分布直方图补充完整；
3. （3）求扇形统计图中 $\text{[math]}$ 部分所对应的扇形圆心角度数；
4. （4）身高在 $\text{[math]}$ 的5人中，甲班有3人，乙班有2人，现从中随机抽取两人补充到学校国旗队．请用列表法或画树状图法，求这两人来自同一班级的概率．
答案解析收藏纠错 + 选题
19. (2022·五莲模拟) 在我市“青山绿水”行动中，某社区计划对面积为 $\text{[math]}$ 的区域进行绿化，经投标由甲、乙两个工程队来完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，如果两队各自独立完成面积为 $\text{[math]}$ 区域的绿化时，甲队比乙队少用6天．
1. （1）求甲、乙两工程队每天各能完成多少面积的绿化；
2. （2）若甲队每天绿化费用是1.2万元，乙队每天绿化费用为0.5万元，社区要使这次绿化的总费用不超过40万元，则至少应安排乙工程队绿化多少天？
答案解析收藏纠错 + 选题
20. (2021九上·单县期中) 如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．
1. （1）求证：直线DF是⊙O的切线；
2. （2）求证：BC²＝4CF•AC；
3. （3）若⊙O的半径为4，∠CDF＝15°，求阴影部分的面积．
答案解析收藏纠错 + 选题
21. (2022·五莲模拟)
1. （1）思维启迪：
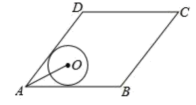
  如图1，A，B两点分别位于一个池塘的两端，小亮想用绳子测量A，B间的距离，但绳子不够长，聪明的小亮想出一个办法：先在地上取一个可以直接到达B点的点C，连接BC，取BC的中点P（点P可以直接到达A点），利用工具过点C作CD∥AB交AP的延长线于点D，此时测得CD＝200米，那么A，B间的距离是米．
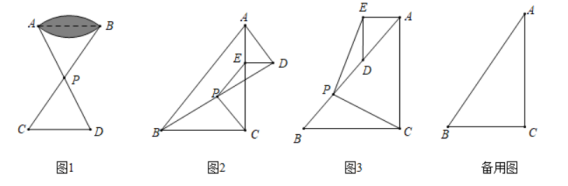
2. （2）思维探索：在△ABC和△ADE中，AC＝BC，AE＝DE，且AE＜AC，∠ACB＝∠AED＝90°，将△ADE绕点A顺时针方向旋转，把点E在AC边上时△ADE的位置作为起始位置（此时点B和点D位于AC的两侧），设旋转角为α，连接BD，点P是线段BD的中点，连接PC，PE．
  ①如图2，当△ADE在起始位置时，猜想：PC与PE的数量关系和位置关系分别是 ▲ ；
  ②如图3，当α＝90°时，点D落在AB边上，请判断PC与PE的数量关系和位置关系，并证明你的结论；
  ③当α＝150°时，若BC＝3，DE＝l，请直接写出PC²的值．
答案解析收藏纠错 + 选题
22. (2022·五莲模拟) 如图，在平面直角坐标系中，抛物线y=ax²+bx+c与 $\text{[math]}$ 轴交于点A（-2，0），点B（4，0），与y轴交于点C（0，8），连接BC，又已知位于y轴右侧且垂直于x轴的动直线 $\text{[math]}$ ，沿x轴正方向从O运动到B（不含O点和B点），且分别交抛物线，线段BC以及x轴于点P、D、E．
1. （1）求抛物线的表达式；
2. （2）连接AC，AP，当直线 $\text{[math]}$ 运动时，求使得△PEA和△AOC相似的点P的坐标；
3. （3）作PF⊥BC，垂足为F，当直线 $\text{[math]}$ 运动时，求Rt△PFD面积的最大值．
答案解析收藏纠错 + 选题