浙江省嘉兴市秀洲区2022年中考二模数学试卷

更新时间：2022-07-04 浏览次数：153 类型：中考模拟

一、选择题（本题有10小题，每小题3分，共30分．请选出各题中唯一的正确选项，不选、多选、错选，均不给分）

1. (2024九下·易门模拟) 下列各组数中，比0小的数是（）

A . 5 B . $\text{[math]}$ C . 0 D . -5

答案解析收藏纠错 + 选题
2. (2022·秀洲模拟) 下列计算正确的是（）

A . a+ 2a= 3a B . （a+b）²=a²+b² C . （a²）³=a⁵ D . a²·a³=a⁶

答案解析收藏纠错 + 选题
3. (2022·秀洲模拟) 如图的几何体由5个同样大小的正方体搭成，它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·秀洲模拟) 2021年嘉兴市国内生产总值（GDP）约6355亿元，比上年增长8.5%，数据6355亿用科学记数法表示为（）

A . 6.35×10¹⁰ B . 0.6355×10¹¹ C . 6.355×10¹² D . 6.355×10¹¹

答案解析收藏纠错 + 选题
5. (2024·南湖模拟) 如图，现有四张正面印有冬奥会吉祥物的不透明卡片，卡片除正面图案不同外，其余均相同，其中两张正面印有冰墩墩图案，两张正面印有雪容融图案，将四张卡片正面向下洗匀，从中随机抽取两张卡片，则抽出的两张卡片图案都是冰墩墩的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·秀洲模拟) 对于实数a，b，定义一种运算“ $\text{[math]}$ ”： a $\text{[math]}$ b=a²-ab，那么不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2024·南湖模拟) 如图，在平面直角坐标系中，以P （0，-1）为位似中心，在y轴右侧作△ABP放大2倍后的位似图形△DCP，若点B的坐标为（-2，-4），则点B的对应点C的坐标为（）

A . （4，5） B . （4，6） C . （2，4） D . （2，6）

答案解析收藏纠错 + 选题
8. (2022·秀洲模拟) 如图，扇形AOB中，∠AOB=90°，OB= $\text{[math]}$ ，点C为AO上一点，将扇形AOB沿着BC折叠，弧A'B恰好经过点O，则阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·南湖模拟) 如图，点F，G分别在正方形ABCD的边BC，CD上，E为AB中点，连结ED，正方形FGQP的边PQ恰好在DE上，记正方形ABCD面积为S₁ ，正方形FPQG面积为S₂ ，则S₁：S₂的值为（）

A . 10：7 B . 20：7 C . 49：10 D . 49：20

答案解析收藏纠错 + 选题
10. (2022·秀洲模拟) 二次函数y=x²-2mx+10图象上一点4（a，b），当3≤a≤5时，存在b=0，则m的取值范围为（）

A . 3≤m≤ $\text{[math]}$ B . $\text{[math]}$ ≤m≤ $\text{[math]}$ C . $\text{[math]}$ ≤m≤ $\text{[math]}$ D . $\text{[math]}$ ≤m≤ $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本愿有6小题，每小题4分，共24分）

11. (2024·南湖模拟) 分解因式： m²-9=

答案解析收藏纠错 + 选题
12. (2024·南湖模拟) 数据3，2，2，3，1的中位数是

答案解析收藏纠错 + 选题
13. (2024·南湖模拟) 在Rt△ABC中，∠C=90°，AC：BC=1：2，则sinB的值为

答案解析收藏纠错 + 选题
14. (2022·秀洲模拟) 如图，在△ABC中，AD为∠CAB的平分线，DE∥AB，若DE=3，CE=4，则AB的值

答案解析收藏纠错 + 选题
15. (2022·秀洲模拟) 某班同学到距学校12千米的森林公园植树，一部分同学骑自行车先行，半小时后，其余同学乘汽车出发，结果他们同时到达，已知汽车的速度是自行车速度的3倍，求自行车和汽车的速度。设自行车的速度为x千米时，则根据题意可列方程为

答案解析收藏纠错 + 选题
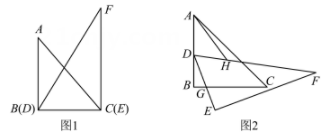
16. (2024·南湖模拟) 一副含45°和30°角的直角三角形纸板ABC和DEF按图1摆放，BC=DE=12，∠ABC= ∠DEF=90°．现将点D从B点向A点滑动，边DE始终经过BC上一点G，BG=2。H是DF边上一点，满足DH=DG（如图2），当点E到达G点时运动停止。当E到达G点时BD的长为；运动过程中AH的最小值是．

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，第17~19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）友情提示：做解答题，别忘了写出必要的过程；作图（包括添加辅助线）：究|最后必须用黑色字迹的签字笔或钢笔将线条描黑

17. (2022·秀洲模拟)
1. （1）计算：2^-1-2022⁰+ sin30°
2. （2）解方程组： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2024九下·嘉兴模拟) 先化简，再求值： $\text{[math]}$ ，其中a=4．

答案解析收藏纠错 + 选题
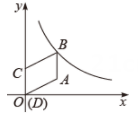
19. (2022·秀洲模拟) 如图，在平面直角坐标系中， ▱ ABCD的顶点D与原点O重合。点C在y轴正半轴上，点B在反比例函数y= $\text{[math]}$ （k >1）的图象上，已知CD=2，点A坐标为（2，1）．
1. （1）求k的值．
2. （2）将 ▱ ABCD沿x轴正方向平移，当A点落在反比例函数图象上时，求平移的距离．
答案解析收藏纠错 + 选题

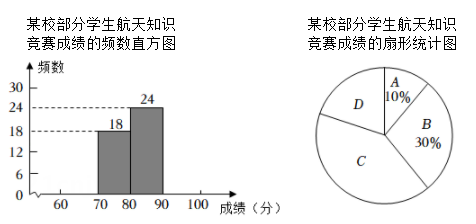
20. (2022·秀洲模拟) 为了培养学生对航天知识的学习兴趣，某校组织全校1200 名学生进行“航天知识竞赛”，从中随机抽取n名学生的竞赛成绩（满分100分，每名学生的成绩记为x分）分成四组，A组： 60≤x<70； B组： 70≤x< 80； C组： 80≤x<90； D组： 90≤x< 100，得到如下不完整的频数表、频数直方图和扇形统计图。根据图中信息，解答下列问题：

aa（某校部分学生航天知识竞赛成绩的频数表

分组	频数
A：60≤x< 70	a
B：70≤x<80	18
C：80≤x<90	24
D：90≤x<100	b

（1） n的值为，a的值为，b的值为
（2）请补全频数直方图，并求图中表示“C”的扇形圆心角的度数．
（3）若规定学生竞赛成绩x≥80为优秀，请估算全校竞赛成绩达到优秀的学生人数．

答案解析收藏纠错 + 选题

21. (2024·南湖模拟) 如图，在菱形ABCD中，∠BAD>90°，P为AC，BD的交点，⊙O经过A，B，P三点．
1. （1）求证：AB为⊙O的直径，
2. （2）请用无刻度的直尺在圆上找一点Q，使得BP=PQ（不写作法，保留作图痕迹）．
答案解析收藏纠错 + 选题
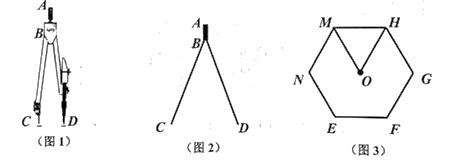
22. (2024·南湖模拟) 如图1是学生常用的一种圆规，其手柄AB=8mm，两脚BC=BD=56mm，如图2所示．当∠CBD=74°时：
1. （1）求A离纸面CD的距离．
2. （2）用该圆规作如图3所示正六边形，求该正六边形的周长．
  （参考数据：sin37°≈0.60，cos37°≈0.80，sin74°≈0.96，cos74°≈0.28，结果精确到0.1）
答案解析收藏纠错 + 选题
23. (2022·秀洲模拟) 某公司成功开发出一种产品，正式投产后，生产成本为5元/件．公司按订单生产该产品（销售量=产量），年销售量y（万件）与售价x （元/件）之间满足如图1所示的函数关系，公司规定产品售价不超过15元/件，受产能限制，年销售量不超过30万件，为了提高该产品竞争力，投入研发费用P元（P万元计入成本），P与x之间的函数关系式如图2所示，当10≤x≤15时可看成抛物线P= $\text{[math]}$ x²-4x+m ．
1. （1）求与x之间的函数关系式。
2. （2）求这种产品年利润W（万元）与售价x（元件）满足的函数关系式．
3. （3）当售价x为多少元时，年利润W最大，并求出这个最大值．
答案解析收藏纠错 + 选题
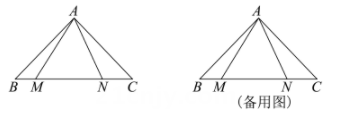
24. (2024·南湖模拟) 如图，Rt△ABC中，AB=AC，∠BAC=90°，BC=6cm，点M，N是边BC上的两个动点，点M从点B出发沿着BC以每秒1cm的速度向终点C运动；点N同时从点C出发沿着CB以每秒2cm的速度向终点B运动．设运动时间为t秒．
1. （1）当t=1时，求△AMN的面积。
2. （2）当t为何值时，∠MAN=45°．
3. （3）当以MN为直径的圆与△AMN的边有且只有三个公共点时，请直接写出t的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省嘉兴市秀洲区2022年中考二模数学试卷

副标题：

*注意事项：

浙江省嘉兴市秀洲区2022年中考二模数学试卷

试题分析

总体分析

题量分析

难度分析

知识点分析