一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
-
2.
(2022·全国甲卷)
某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:
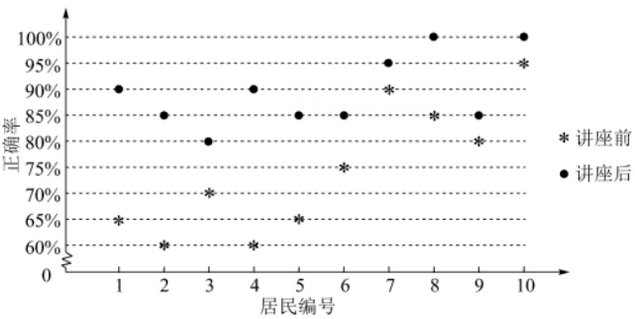
则( )
A . 讲座前问卷答题的正确率的中位数小于70%
B . 讲座后问卷答题的正确率的平均数大于85%
C . 讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D . 讲座后问卷答题的正确率的极差大于讲座前正确率的极差
-
-
4.
(2022·全国甲卷)
如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )
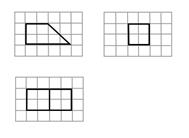
A . 8
B . 12
C . 16
D . 20
-
5.
(2025·)
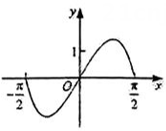
将函数

的图像向左平移

个单位长度后得到曲线C,若C关于y轴对称,则

的最小值是( )
-
6.
(2024高二上·杭州期中)
从分别写有1,2,3,4,5,6的6张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之积是4的倍数的概率为( )
-
-
A . -1
B .  C .
C .  D . 1
D . 1
-
A .  B . AB与平面
B . AB与平面  所成的角为
所成的角为  C .
C .  D .
D .  与平面
与平面  所成的角为
所成的角为 
-
10.
(2022·全国甲卷)
甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为

,侧面积分别为

和

,体积分别为

和

.若

,则

( )
-
11.
(2022·全国甲卷)
已知椭圆

的离心率为

,

分别为C的左、右顶点,B为C的上顶点.若

,则C的方程为( )
-
12.
已知

,则( )
二、填空题:本题共4小题,每小题5分,共20分。
-
-
-
-
16.
(2025·)
已知

中,点D在边BC上,

.当

取得最小值时,

.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
-
17.
(2022·全国甲卷)
甲、乙两城之间的长途客车均由A和B两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:
|
|
准点班次数
|
未准点班次数
|
|
A
|
240
|
20
|
|
B
|
210
|
30
|
附:  ,
,
|  | 0.100 | 0.050 | 0.010 |
|  | 2.706 | 3.841 | 6.635 |
-
(1)
根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;
-
(2)
能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?
-
-
(1)
证明:

是等差数列;
-
(2)
若

成等比数列,求

的最小值.
-
19.
(2022·全国甲卷)
小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面

是边长为8(单位:cm)的正方形,

均为正三角形,且它们所在的平面都与平面

垂直.
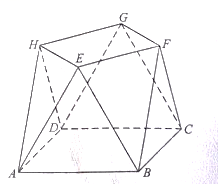
-
(1)
证明:

平面

;
-
(2)
求该包装盒的容积(不计包装盒材料的厚度).
-
-
(1)
若

,求a:
-
-
21.
(2022·全国甲卷)
设抛物线

的焦点为F,点

,过

的直线交C于M,N两点.当直线MD垂直于x轴时,

.
-
-
(2)
设直线

与C的另一个交点分别为A,B,记直线

的倾斜角分别为

.当

取得最大值时,求直线AB的方程.
四、选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
-
22.
(2022·全国甲卷)
在直角坐标系

中,曲线

的参数方程为

(t为参数),曲线

的参数方程为

(s为参数).
-
(1)
写出

的普通方程;
-
(2)
以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线

的极坐标方程为

,求

与

交点的直角坐标,及

与

交点的直角坐标.
-


 B .
B . 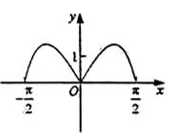 C .
C . 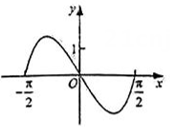 D .
D . 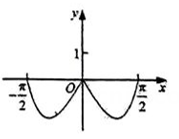
,