2012年高考理数真题试卷（江西卷）

更新时间：2021-05-20 浏览次数：254 类型：高考真卷

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2012·江西理) 若集合A={﹣1，1}，B={0，2}，则集合{z|z=x+y，x∈A，y∈B}中的元素的个数为（）

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
2. (2012·江西理) 下列函数中，与函数y= $\text{[math]}$ 定义域相同的函数为（）

A . y= $\text{[math]}$ B . y= $\text{[math]}$ C . y=xe^x D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2012·江西理) 若函数f（x）= $\text{[math]}$ ，则f（f（10））=（）

A . lg101 B . 2 C . 1 D . 0

答案解析收藏纠错 + 选题
4. (2012·江西理) 若tanθ+ $\text{[math]}$ =4，则sin2θ=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2012·江西理) 下列命题中，假命题为（）

A . 存在四边相等的四边形不是正方形 B . z₁ ， z₂∈C，z₁+z₂为实数的充分必要条件是z₁ ， z₂互为共轭复数 C . 若x，y∈R，且x+y＞2，则x，y至少有一个大于1 D . 对于任意n∈N^* ， $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ 都是偶数

答案解析收藏纠错 + 选题
6. (2012·江西理) 观察下列各式：a+b=1，a²+b²=3，a³+b³=4，a⁴+b⁴=7，a⁵+b⁵=11，…，则a¹⁰+b¹⁰=（）

A . 28 B . 76 C . 123 D . 199

答案解析收藏纠错 + 选题
7. (2020高二上·上海月考) 在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则 $\text{[math]}$ =（）

A . 2 B . 4 C . 5 D . 10

答案解析收藏纠错 + 选题
8. (2012·江西理) 某农户计划种植黄瓜和韭菜，种植面积不超过50亩，投入资金不超过54万元，假设种植黄瓜和韭菜的产量、成本和售价如下表
年产量/亩
年种植成本/亩
每吨售价
黄瓜
4吨
1.2万元
0.55万元
韭菜
6吨
0.9万元
0.3万元
为使一年的种植总利润（总利润=总销售收入﹣总种植成本）最大，那么黄瓜和韭菜的种植面积（单位：亩）分别为（）

A . 50，0 B . 30，20 C . 20，30 D . 0，50

答案解析收藏纠错 + 选题
9. (2012·江西理) 样本（x₁ ， x₂…，x_n）的平均数为x，样本（y₁ ， y₂ ， …，y_m）的平均数为 $\text{[math]}$ （ $\text{[math]}$ ≠ $\text{[math]}$ ）．若样本（x₁ ， x₂…，x_n ， y₁ ， y₂ ， …，y_m）的平均数 $\text{[math]}$ =α $\text{[math]}$ +（1﹣α） $\text{[math]}$ ，其中0＜α＜ $\text{[math]}$ ，则n，m的大小关系为（）

A . n＜m B . n＞m C . n=m D . 不能确定

答案解析收藏纠错 + 选题
10. (2012·江西理) 如图，已知正四棱锥S﹣ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE=x（0＜x＜1），截面下面部分的体积为V（x），则函数y=V（x）的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题

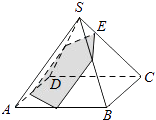
二、填空题

11. (2012·江西理) 计算定积分 $\text{[math]}$ （x²+sinx）dx=．

答案解析收藏纠错 + 选题
12. 设数列{a_n}，{b_n}都是等差数列，若a₁+b₁=7，a₃+b₃=21，则a₅+b₅=．

答案解析收藏纠错 + 选题
13. (2012·江西理) 椭圆 $\text{[math]}$ + $\text{[math]}$ =1（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F₁ ， F₂ ．若|AF₁|，|F₁F₂|，|F₁B|成等比数列，则此椭圆的离心率为．

答案解析收藏纠错 + 选题
14. (2012·江西理) 下图是某算法的程序框图，则程序运行后输出的结果是．

答案解析收藏纠错 + 选题

三、选做题：请在下列两题中任选一题作答．若两题都做，则按第一题评阅计分

15. (2012·江西理)
1. （1）（坐标系与参数方程选做题）曲线C的直角坐标方程为x²+y²﹣2x=0，以原点为极点，x轴的正半轴为极轴建立积坐标系，则曲线C的极坐标方程为．
2. （2）（不等式选做题）在实数范围内，不等式|2x﹣1|+|2x+1|≤6的解集为．
答案解析收藏纠错 + 选题

四、解答题．解答应写出文字说明、证明过程或演算步骤．

16. (2012·江西理) 已知数列{a_n}的前n项和S_n=﹣ $\text{[math]}$ n²+kn（其中k∈N₊），且S_n的最大值为8．
1. （1）确定常数k，求a_n；
2. （2）求数列 $\text{[math]}$ 的前n项和T_n ．
答案解析收藏纠错 + 选题
17. (2012·江西理) 在△ABC中，角A，B，C的对边分别为a，b，c．已知A= $\text{[math]}$ ，bsin（ $\text{[math]}$ +C）﹣csin（ $\text{[math]}$ +B）=a，
1. （1）求证：B﹣C= $\text{[math]}$
2. （2）若a= $\text{[math]}$ ，求△ABC的面积．
答案解析收藏纠错 + 选题
18. (2012·江西理) 如图，从A₁（1，0，0），A₂（2，0，0），B₁（0，1，0），B₂（0，2，0），C₁（0，0，1），C₂（0，0，2）这6个点中随机选取3个点，将这3个点及原点O两两相连构成一个“立体”，记该“立体”的体积为随机变量V（如果选取的3个点与原点在同一个平面内，此时“立体”的体积V=0）．
1. （1）求V=0的概率；
2. （2）求V的分布列及数学期望EV．
答案解析收藏纠错 + 选题
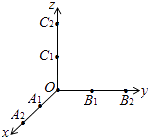
19. (2012·江西理) 在三棱柱ABC﹣A₁B₁C₁中，已知AB=AC=AA₁= $\text{[math]}$ ，BC=4，点A₁在底面ABC的投影是线段BC的中点O．
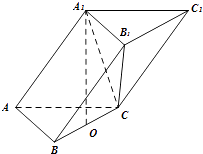
1. （1）证明在侧棱AA₁上存在一点E，使得OE⊥平面BB₁C₁C，并求出AE的长；
2. （2）求平面A₁B₁C与平面BB₁C₁C夹角的余弦值．
答案解析收藏纠错 + 选题
20. (2012·江西理) 已知三点O（0，0），A（﹣2，1），B（2，1），曲线C上任意一点M（x，y）满足| $\text{[math]}$ + $\text{[math]}$ |= $\text{[math]}$ •（ $\text{[math]}$ + $\text{[math]}$ ）+2．
1. （1）求曲线C的方程；
2. （2）动点Q（x₀ ， y₀）（﹣2＜x₀＜2）在曲线C上，曲线C在点Q处的切线为直线l：是否存在定点P（0，t）（t＜0），使得l与PA，PB都相交，交点分别为D，E，且△QAB与△PDE的面积之比是常数？若存在，求t的值．若不存在，说明理由．
答案解析收藏纠错 + 选题
21. (2012·江西理) 若函数h（x）满足
①h（0）=1，h（1）=0；
②对任意a∈[0，1]，有h（h（a））=a；
③在（0，1）上单调递减．则称h（x）为补函数．已知函数h（x）= $\text{[math]}$ （λ＞﹣1，p＞0）
1. （1）判函数h（x）是否为补函数，并证明你的结论；
2. （2）若存在m∈[0，1]，使得h（m）=m，若m是函数h（x）的中介元，记p= $\text{[math]}$ （n∈N₊）时h（x）的中介元为x_n ，且S_n= $\text{[math]}$ ，若对任意的n∈N₊ ，都有S_n＜ $\text{[math]}$ ，求λ的取值范围；
3. （3）当λ=0，x∈（0，1）时，函数y=h（x）的图象总在直线y=1﹣x的上方，求P的取值范围．
答案解析收藏纠错 + 选题