 B .
B .  C .
C . 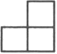 D .
D . 


等级 | 成绩x/分 | 人数 |
A | 90≤x≤100 | 15 |
B | 80≤x<90 | a |
C | 70≤x<80 | 18 |
D | x<70 | 7 |
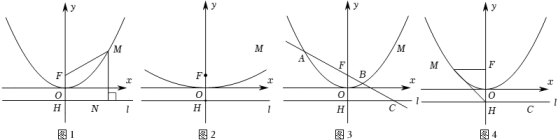
请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程:,.
如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
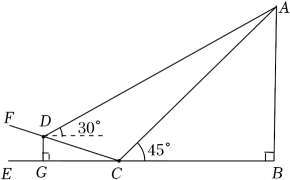
如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值;
古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:=
=
.后人把
这个数称为“黄金分割”把点C称为线段AB的黄金分割点.
如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,﹣1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当
=
时,请直接写出△HME的面积值.