山西省阳泉市2022年中考考前教学质量检测（一模）数学试题

更新时间：2024-07-13 浏览次数：67 类型：中考模拟

一、单选题

1. (2022·阳泉模拟) 在 $\text{[math]}$ ， $\text{[math]}$ ， 0， $\text{[math]}$ 这四个数中，为无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . -2

答案解析收藏纠错 + 选题
2. (2023九下·永丰期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·阳泉模拟) 下列图形中，主视图为①的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·阳泉模拟) 北京作为全球首个双奥之城，于2月4日至2月20日举办第24届冬奥会，本届冬奥会汇聚了世界各国的运动员．伴随着中国以及数字媒体的发展，北京冬奥会创造了多项纪录：数字化互动最广泛的冬奥会、转播时长最长的冬奥会以及开幕式收视率最高的冬奥会．在赛事期间，创纪录的6400多万人使用奥林匹克网站和App关注冬奥会．数字6400万用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·龙马潭开学考) 甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示，如果从这四位同学中，选出一位同学参加数学竞赛，那么应选___________去.

甲

乙

丙

丁

平均分

85

90

90

85

方差

50

42

50

42

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
6. (2022·阳泉模拟) 把不等式组 $\text{[math]}$ 中每个不等式的解集在同一条数轴上表示出来，正确的为（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022·阳泉模拟) 如图，在“3×3”网格中，有3个涂成黑色的小方格．若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称图案的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·信阳模拟) 如图，点O为菱形ABCD的对角线AC，BD的交点，过点C作CE⊥AB于点E，连接OE，若OD＝3，OE＝2，则菱形ABCD的面积为（）

A . 6 B . 12 C . 18 D . 24

答案解析收藏纠错 + 选题
9. (2022·阳泉模拟) 如图，点P是反比例函数 $\text{[math]}$ 的图象上一点，过点P作PA⊥y轴于点A，点B是点A关于x轴的对称点，连接PB，若△PAB的面积为6，则k的值为（）

A . －3 B . 6 C . －6 D . －12

答案解析收藏纠错 + 选题
10. (2022·阳泉模拟) 如图，在扇形AOB中，∠AOB＝120°，半径OC交弦AB于点D，且OC⊥OA．若 $\text{[math]}$ ，则阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·诸暨期末) 方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
12. (2022·阳泉模拟) 如图，含30°角的直角三角板的直角顶点C落在直尺下边沿上，60°角的顶点A落在直尺上边沿，直角边CD与直尺上边沿交于点B．若∠1＝33°，则∠2＝．

答案解析收藏纠错 + 选题
13. (2022·阳泉模拟) 某中学有一块长30m，宽20m的矩形空地，计划在这块空地上划分出四分之一的区域种花，小明同学设计方案如图所示，求花带的宽度．设花带的宽为xm，则可列方程为．

答案解析收藏纠错 + 选题
14. (2022·阳泉模拟) 如图，已知 $\text{[math]}$ 是等腰三角形， $\text{[math]}$ 点D在AC边上，将 $\text{[math]}$ 绕点A逆时针旋转45°得到 $\text{[math]}$ ，且点D′、D、B三点在同一条直线上，则 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
15. (2022·阳泉模拟) 如图，边长为 $\text{[math]}$ 的正方形ABCD中，点E为对角线BD上一点，连接CE，将CE绕点C顺时针旋转90°得到CF，连接EF和DF若EF＝2BE，则BE的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2022·阳泉模拟) 计算及先化简求值
1. （1） $\text{[math]}$ ；
2. （2）先化简 $\text{[math]}$ ，再选一个合适的x的值代入求值．
答案解析收藏纠错 + 选题
17. (2022·阳泉模拟) 如图，点O为Rt△ABC的斜边BC上一点，以点O为圆心、OC为半径的⊙O与边AB相切于点D，与边AC，BC分别相交于点E，F，连接OE，DE，DF．
1. （1）求证：DE＝DF；
2. （2）若∠B＝30°，⊙O的半径为8，求AC的长．
答案解析收藏纠错 + 选题
18. (2022·阳泉模拟) 某校组织了九年级学生进行“汉字听写大赛”，据统计，所有学生的比赛成绩均超过60分，最高分为100分．比赛的成绩分以下四个等级：A（ $\text{[math]}$ ），B（ $\text{[math]}$ ），C（ $\text{[math]}$ ），D（ $\text{[math]}$ ）（单位：分）．现随机抽取了九年级若干名学生的比赛成绩，绘制出如下不完整的统计图．请你结合以上信息，解答下列问题：
1. （1）请补全比赛成绩直方图；
2. （2）针对本次统计结果，以下三位同学做出如下判断：
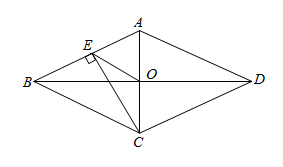
  小强认为：中位数落在B组；
  小明认为：众数落在C组；
  小亮认为：若C组有a人，则可估算平均成绩约为： $\text{[math]}$ ．
  以上判断中有一位同学是错误的，这位同学是（填“小强”、“小明”或“小亮”）；
3. （3）若该校九年级共1000名学生，测试成绩高于80分记为“优秀”，请你估计该校九年级学生中汉字听写比赛成绩达到“优秀”的人数．
4. （4）学校要求，各班需推荐一男一女两名学生参加总决赛，九年级（2）班班主任要在本班前五名同学（包括两名男生和三名女生）中进行推选，请用列表或树状图求恰好能按要求推选的概率是多少？
答案解析收藏纠错 + 选题
19. (2022·阳泉模拟) 健康绿色生活，从饮用水开始！随着科技的发展和生活质量的不断提高，人们的自我保健意识也不断增强，对饮水品质的需求也越来越高．我市某公司根据市场需求代理A，B两种型号的净水器，每台A型净水器比每台B型净水器进价多200元，用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等．
1. （1）求每台A型、B型净水器的进价各是多少元？
2. （2）该公司计划购进A、B两种型号的净水器共50台进行试销，其中A型净水器为x台，购买资金不超过9.8万元．试销时A型净水器每台售价2500元，B型净水器每台售价2180元，该公司决定从销售A型净水器的利润中按每台捐献75元作为公司帮扶贫困村饮水改造资金，设该公司售完50台净水器并捐献扶贫资金后获得的利润为W，求W的最大值．
答案解析收藏纠错 + 选题
20. (2022·阳泉模拟) 随着科技的发展，越来越多高科技的产品应用在我们的生活中，智能跟踪监控摄像头就是其中的一种（如图1）．一款被安装在某小区住宅楼铅直墙面l上A处的跟踪摄像头，在捕捉到地面上E处有一跟踪目标时，数据显示该目标到摄像头水平距离BE＝8m，此时摄像头的俯视角度 $\text{[math]}$ 为35°；继续跟踪目标到达围墙CD的墙头D处，此时摄像头俯视角度减小了15°．已知围墙CD的铅直高度为1.8m，请求出目标落脚点D到墙面l的水平距离（结果保留到0.1m）．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

21. (2022·阳泉模拟) 阅读下列材料，完成相应的学习任务．

巧折黄金矩形

如果一个矩形宽与长的比为 $\text{[math]}$ ，那么这样的矩形叫做黄金矩形．

我们可以用如下方法折出黄金矩形：

如图，在矩形纸片ABCD中，AD＝2．

操作1：将矩形纸片ABCD沿AF折叠，使得点D落在AB上的点E处，

展开得到折痕AF；

操作2：再将该矩形纸片折叠，使得点D与点F重合，展开得到折痕GH；

操作3：继续折叠该纸片，使得AG落在DC上，点A的对应点为点M，

点D的对应点为点P，折痕为GQ；

操作4：过点M折出DC的垂线，折痕为MN．

则四边形FENM是黄金矩形．

学习任务：

（1）请你证明四边形FENM是黄金矩形；
（2）在不添加其他字母的情况下，请你再写出图中的一个黄金矩形．（参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题

22. (2022·阳泉模拟) 综合与实践
【问题背景】
如图1，平行四边形ABCD中，∠B＝60°，AB＝6，AD＝8．点E、G分别是AD和DC边的中点，过点E、G分别作DC和AD的平行线，两线交于点F，显然，四边形DEFG是平行四边形．
【独立思考】
1. （1）线段AE和线段CG的数量关系是：．
2. （2）将平行四边形DEFG绕点D逆时针旋转，当DE落在DC边上时，如图2，连接AE和CG．
  ①求AE的长；
  ②猜想AE与CG有怎样的数量关系，并证明你的猜想；
3. （3）【问题解决】
  将平行四边形DEFG继续绕点D逆时针旋转，当A，E，F三点在同一直线上时（如图3），AE与CG交于点P，请直接写出线段CG的长和∠APC的度数．
答案解析收藏纠错 + 选题
23. (2022·阳泉模拟) 综合与探究
如图，已知抛物线 $\text{[math]}$ 与x轴负半轴交于点 $\text{[math]}$ ，与y轴交于点 $\text{[math]}$ ，抛物线的顶点为D，直线y＝x＋b与抛物线交于A，F两点，过点D作DE∥y轴交直线AF于点E．
1. （1）求抛物线和直线AF的解析式；
2. （2）在直线AF上方的抛物线上有一点P，使 $\text{[math]}$ ，求点P的坐标；
3. （3）若点M为抛物线上一动点，试探究在直线AF上是否存在一点N，使得以D，E，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题