B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

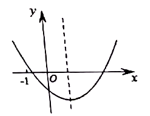
①这组数据的众数是8;
②这组数据的中位数是7;
③这组数据的平均数是7;
④这组数据的方差是2.2
成绩(次) | 9 | 8 | 6 | 5 |
人数(名) | 2 | 3 | 3 | 2 |
,其中x是不等式组
的一个整数解.
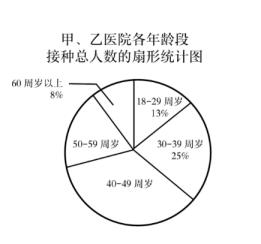
甲医院 | 乙医院 | |||
年龄段 | 频数 | 频率 | 频数 | 频率 |
18—29周岁 | 900 | 0.15 | 400 | 0.1 |
30—39周岁 | a | 0.25 | 1000 | 0.25 |
40—49周岁 | 2100 | b | c | 0.225 |
50—59周岁 | 1200 | 0.2 | 1200 | 0.3 |
60周岁以上 | 300 | 0.05 | 500 | 0.125 |
①填空:a=,b=,c=;
②在甲、乙两医院当天接种疫苗的所有人员中,40—49周岁年龄段人数在扇形统计图中所占圆心角为;
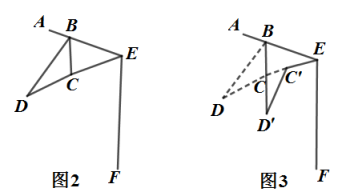
①作线段 的垂直平分线
,分别交
于点
于点
,连接
;
②以点 为圆心,
长为半径作弧,交
于点
(
两点不重合),连接
.
(参考数据: ,
,
,
,
,
)
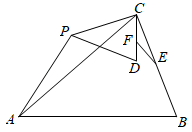
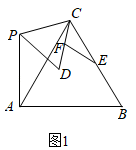
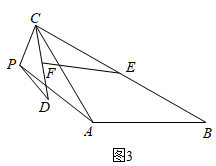
如图,已知△ABC中, ,
,
, 点P为平面内不与点A,C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转
, 得线段PD,连接CD,AP.点E,F分别为BC,CD的中点,设直线AP与直线EF相交所成的较小角为
, 探究
的值AB和
的度数.