 B .
B . 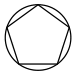 C .
C . 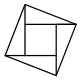 D .
D . 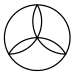
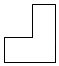 B .
B .  C .
C . 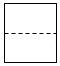 D .
D . 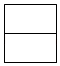

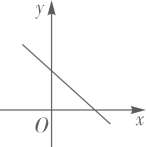 B .
B . 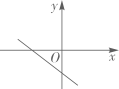 C .
C . 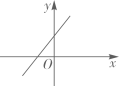 D .
D . 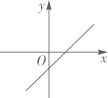


选项 | 学习时间t(小时) |
A | |
B | |
C | |
D |

(参考数据: ,
,
,
,
,
)

月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量 | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
7至12月,该企业自身处理的污水量(吨)与月份x(
, 且x取整数)之间满足二次函数关系式
, 其图象如图所示.

1至6月,污水厂处理每吨污水的费用:(元)与月份x之间满足函数关系式:
, 该企业自身处理每吨污水的费用:
(元)与月份x之间满足函数关系式:
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
②7至12月,该企业哪个月用于污水处理的费用W(元)最多?
③该企业全年哪个月用于污水处理的费用W(元)最多?请求出这个最多费用.

探究一:
从简单情况入手:
如果只有1,2,很明显,留下1,擦去2,最后剩下1;
如果只有1,2,3,4,如图所示,第一圈留下1,3擦去2,4;第二圈留下1,擦去3,最后剩下1;
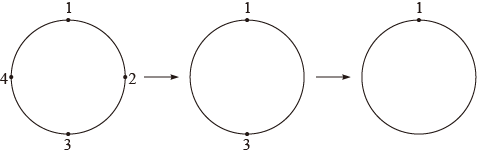
如果只有1,2,3,4,5,6,7,8,如图所示,第一圈留下1,3,5,7擦去2,4,6,8;第二圈留下1,5擦去3,7;第三圈留下1,擦去5;最后剩下1;

问题一:如果只有1,2,3,…,16这16个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4…(每隔一数,擦去一数),转圈擦下去,最后剩下的数是;
探究二:
如果只有1,2,3,4,5,6,7这7个数,由探究一可知只有4个数时,最后剩下的是1,即4个数中的“第一个数”,因此只要剩下4个数,即可知最后剩下的是哪个数.也就是先擦掉个数,擦掉的第3个数是6,它的下一个数是7,也就是剩下的4个数中的第一个是7,所以最后剩下的数就是7;
如果只有1,2,3,…,12这12个数,由探究一可知只有8个数时,最后剩下的是1,即8个数中的“第一个数”,因此只要剩下8个数,即可知最后剩下的是哪个数.也就是先擦掉个数,擦掉的第4个数是8,它的下一个数是9,也就是剩下的8个数中的第一个是9,所以最后剩下的数就是9;
仿照上面的探究方法,回答下列问题:
问题二,如果只有1,2,3,…,26这26个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,最后剩下的数是;
问题解决:
问题三:把1到2022这2022个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,最后剩下的数是;
一般归纳:
问题四:把1,2,3,…,n这个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,如果 , 且n和k都是正整数,则最后剩下的数是;(用n、k的代数式表示)
拓展延伸:
问题五:如果只有1,2,3,…,n这n个数,且 , n是正整数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,如果最后剩下的数是2023,则n可以为.
