浙江省历年（2018-2022年）真题分类汇编专题49 数据...

更新时间：2022-10-11 浏览次数：64 类型：二轮复习

一、单选题

1. (2018·湖州) 某工艺品厂草编车间共有16名工人，为了了解每个工人的日均生产能力，随机调查了某一天每个工人的生产件数．获得数据如下表：
生产件数（件）
10
11
12
13
14
15
人数（人）
1
5
4
3
2
1
则这一天16名工人生产件数的众数是（）

A . 5件 B . 11件 C . 12件 D . 15件

答案解析收藏纠错 + 选题
2. (2023九下·长沙月考) 某篮球运动员在连续7场比赛中的得分（单位：分）依次为20，18，23，17，20，20，18，则这组数据的众数与中位数分别是（）

A . 18分，17分 B . 20分，17分 C . 20分，19分 D . 20分，20分

答案解析收藏纠错 + 选题
3. (2021·宜宾模拟) 若一组数据4，1，7，x，5的平均数为4，则这组数据的中位数为（）

A . 7 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
4. (2024九下·高阳模拟) 某校九年级“诗歌大会”比赛中，各班代表队得分如下（单位：分）：9，7，8，7，9，7，6，则各代表队得分的中位数是（）

A . 9分 B . 8分 C . 7分 D . 6分

答案解析收藏纠错 + 选题
5. 2018年1－4月我国新能源乘用车的月销量情况如图所示，则下列说法错误的是（）

A . 1月份销量为2.2万辆 B . 从2月到3月的月销量增长最快 C . 4月份销量比3月份增加了1万辆 D . 1－4月新能源乘用车销量逐月增加

答案解析收藏纠错 + 选题
6. (2019·温州) 对温州某社区居民最爱吃的鱼类进行问卷调查后（每人选一种），绘制成如图所示统计图．已知选择鲳鱼的有40人，那么选择黄鱼的有（）

A . 20人 B . 40人 C . 60人 D . 80人

答案解析收藏纠错 + 选题

7. (2019七上·长兴月考) 某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是（）

星期	一	二	三	四
最高气温	10℃	12℃	11℃	9℃
最低气温	3℃	0℃	-2℃	-3℃

A . 星期一 B . 星期二 C . 星期三 D . 星期四

答案解析收藏纠错 + 选题

8. 点点同学对数据26，36，36，46，5■，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A . 平均数 B . 中位数 C . 方差 D . 标准差

答案解析收藏纠错 + 选题
9. (2021九下·柯桥月考) 测试五位学生“一分钟跳绳”成绩，得到五个各不相同的数据，统计时，出现了一处错误：将最高成绩写得更高了。计算结果不受影响的是（）

A . 方差 B . 标准差 C . 中位数 D . 平均数

答案解析收藏纠错 + 选题
10. (2017·绍兴) 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：

甲
乙
丙
丁
平均数（环）
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

二、填空题

11. (2020·永嘉模拟) 一组数据1，3，2，7， $\text{[math]}$ ，2，3的平均数是3，则该组数据的众数为．

答案解析收藏纠错 + 选题
12. (2022·瑞安模拟) 数据2，7，5，7，9的众数是。

答案解析收藏纠错 + 选题
13. (2019九上·瑞安开学考) 数据3，4，10，7，6的中位数是．

答案解析收藏纠错 + 选题
14. (2018·衢州) 数据5，5，4，2，3，7，6的中位数是·

答案解析收藏纠错 + 选题
15. (2019·温州) 某校学生“汉字听写”大赛成绩的频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，其中成绩为“优良”（80分及以上）的学生有人．

答案解析收藏纠错 + 选题
16. (2019九上·石家庄月考) 学校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班的平均得分是分.

答案解析收藏纠错 + 选题

三、综合题

17. (2018·台州) 某市明年的初中毕业升学考试，拟将“引体向上”作为男生体育考试的一个必考项目，满分为10分.有关部分为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平，在全市八年级男生中随机抽取了部分男生，对他们的“引体向上”水平进行测试，并将测试结果绘制成如下统计图表（部分信息未给出）：
抽取的男生“引体向上”成绩统计表
成绩
人数
0分
32
1分
30
2分
24
3分
11
4分
15
5分及以上
$\text{[math]}$
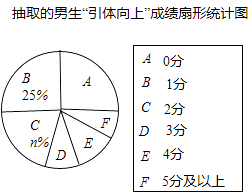
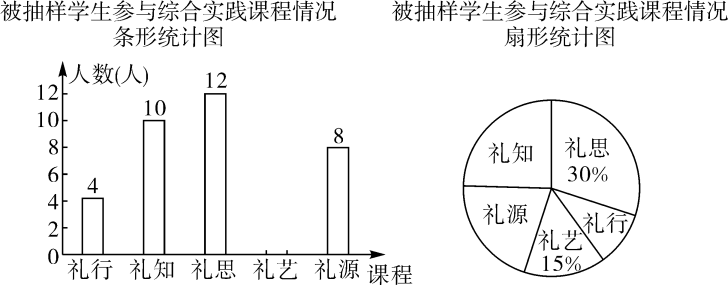
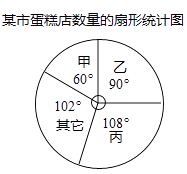
请你根据统计图表中的信息，解答下列问题：
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）求扇形统计图中 $\text{[math]}$ 组的扇形圆心角的度数；
3. （3）目前该市八年级有男生3600名，请估计其中“引体向上”得零分的人数.
答案解析收藏纠错 + 选题
18. (2018·义乌) 为了解某地区机动机拥有量对道路通行的影响，学校九年级社会实践小组对2010年～2017年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计，并绘制成下列统计图：
根据统计图，回答下列问题：
1. （1）写出2016年机动车的拥有量，分别计算2010年～2017年在人民路路口和学校门口堵车次数的平均数.
2. （2）根据统计数据，结合生活实际，对机动车拥有量与人民路路口和学校门口堵车次数，说说你的看法.
答案解析收藏纠错 + 选题
19. (2022八下·东丽期末) 某校积极开展中学生社会实践活动，决定成立文明宣传、环境保护、交通监督三个志愿者队伍，每名学生最多选择一个队伍，为了了解学生的选择意向，随机抽取A，B，C，D四个班，共200名学生进行调查．将调查得到的数据进行整理，绘制成如下统计图（不完整）
1. （1）求扇形统计图中交通监督所在扇形的圆心角度数；
2. （2）求D班选择环境保护的学生人数，并补全折线统计图；（温馨提示：请画在答题卷相对应的图上）
3. （3）若该校共有学生2500人，试估计该校选择文明宣传的学生人数．
答案解析收藏纠错 + 选题
20. (2018·宁波) 在第23个世界读书日前夕，我市某中学为了解本校学生的每周课外阅读时间（用t表示，单位：小时），采用随机抽样的方法进行问卷调查．调查结果按0≤t＜2，2≤t＜3，3≤t＜4，t≥4分为四个等级，并依次用A，B，C，D表示．根据调查结果统计的数据，绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：
1. （1）求本次调查的学生人数；
2. （2）求扇形统计图中等级B所在扇形的圆心角度数，并把条形统计图补充完整；
3. （3）若该校共有学生1200人，试估计每周课外阅读时间满足3≤t＜4的人数．
答案解析收藏纠错 + 选题
21. (2021·萧山模拟) 现有甲、乙、丙等多家食品公司在某市开设蛋糕店，该市蛋糕店数量的扇形统计图如图所示，其中统计图中没有标注相应公司数量的百分比．已知乙公司经营150家蛋糕店，请根据该统计图回答下列问题：
1. （1）求甲公司经营的蛋糕店数量和该市蛋糕店的总数．
2. （2）甲公司为了扩大市场占有率，决定在该市增设蛋糕店数量达到全市的20%，求甲公司需要增设的蛋糕店数量．
答案解析收藏纠错 + 选题
22. (2018·杭州) 某校积极参与垃圾分类活动，以班级为单位收集可回收的垃圾，下面是七年级各班一周收集的可回收垃圾的质量频数和频数直方图（每组含前一个边界值，不含后一个边界值）。
1. （1）求a的值。
2. （2）已知收集的可回收垃圾以0.8元/kg被回收，该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元。
答案解析收藏纠错 + 选题
23. (2018·舟山) 某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为176mm-185mm的产品为合格），随机各轴取了20个样品进行测，过程如下：
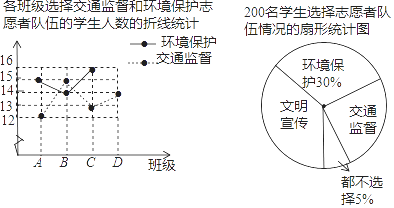
收集数据（单位：mm）：
甲车间：168，175，180，185，172，189，185，182，185，174，192，180，185，178，173，185，169，187，176，180。
乙车间：186，180，189，183，176，173，178，167，180，175，178，182，180，179，185，180，184，182，180，183。
整理数据：

分析数据：
应用数据：
1. （1）计算甲车间样品的合格率。
2. （2）估计乙车间生产的1000个该款新产品中合格产品有多少个？
3. （3）结合上述数据信息，请判断个车间生产的新产品更好，并说明理由，
答案解析收藏纠错 + 选题
24. (2018·绍兴) 为了解某地区机年动车拥有量对道路通行的影响，学校九年级社会实践小组对2010—2017年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计，并绘制成下列统计图：
根据统计图，回答下列问题
1. （1）写出2016年机动车的拥有量，分别计算2010年—2017年在人民路路口和学校门口堵车次数的平均数。
2. （2）根据统计数据，结合生活实际，对机动车拥有量与人民路路口和学校门口堵车次数，说说你的看法。
答案解析收藏纠错 + 选题
25. (2018·衢州) 为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”“文明交通”、“关爱老人”、“义务植树”“社区服务”等五项，活动期间，随机抽取了部分学生对志者服务情况进行调查．结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如所示不完整的折线统计图和扇形统计图。
1. （1）被随机抽取的学生共有多少名？
2. （2）在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；
3. （3）该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？
答案解析收藏纠错 + 选题

26. (2020九下·常州月考) 车间有20名工人，某天他们生产的零件个数统计如下表．

车间20名工人某一天生产的零件个数统计表

生产零件的个数（个）	9	10	11	12	13	15	16	19	20
工人人数（人）	1	1	6	4	2	2	2	1	1

（1）求这一天20名工人生产零件的平均个数；
（2）为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者，从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？

答案解析收藏纠错 + 选题

27. (2019·金华) 某校根据课程设置要求，开设了数学类拓展性课程。为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（生人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整），请根据图中信息回答问题。
1. （1）求m，n的值。
2. （2）补全条形统计图。
3. （3）该校共有1200名学生，试估计全校最喜欢“数学史话”的学生人数。
答案解析收藏纠错 + 选题
28. (2019·湖州) 我市自开展“学习新思想，做好接班人”主题阅读活动以来，受到各校的广泛关注和同学们的积极响应，某校为了解全校学生主题阅读的情况，随机抽查了部分学生在某一周主题阅读文章的篇数，并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表

文章阅读的篇数(篇)

3

4

5

6

7及以上

人数(人)

20

28

m

16

12

某校抽查的学生文章阅读的篇数情况统计图

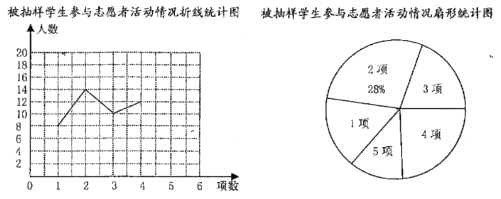
请根据统计图表中的信息，解答下列问题：
1. （1）求被抽查的学生人数和m的值；
2. （2）求本次抽查的学生文章阅读篇数的中位数和众数；
3. （3）若该校共有800名学生，根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
答案解析收藏纠错 + 选题
29. (2019·衢州) 某校为积极响应“南孔圣地，衢州有礼”城市品牌建设，在每周五下午第三节课开展了丰富多彩的走班选课活动。其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程，要求全校学生必须参与其中一门课程。为了解学生参与综合实践类课程活动情况，随机抽取了部分学生进行调查，根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图。
1. （1）请问被随机抽取的学生共有多少名?并补全条形统计图。
2. （2）在扇形统计图中，求选择“礼行”课程的学生人数所对应的扇形圆心角的度数。
3. （3）若该校共有学生1200人，估计其中参与“礼源”课程的学生共有多少人？
答案解析收藏纠错 + 选题
30. (2020·三明模拟) 小明、小聪参加了100m跑的5期集训，每期集训结束时进行测试，根据他们的集训时间、测试成绩绘制成如下两个统计图。

根据图中信息，解答下列问题：
1. （1）这5期的集训共有多少天？小聪5次测试的平均成绩是多少?
2. （2）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，说说你的想法.。
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省历年（2018-2022年）真题分类汇编专题49 数据...

副标题：

*注意事项：

浙江省历年（2018-2022年）真题分类汇编专题49 数据...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

	甲	乙	丙	丁
平均数（环）	9.14	9.15	9.14	9.15
方差	6.6	6.8	6.7	6.6

成绩	人数
0分	32
1分	30
2分	24
3分	11
4分	15
5分及以上	$\text{[math]}$

文章阅读的篇数(篇)	3	4	5	6	7及以上
人数(人)	20	28	m	16	12

生产件数（件）	10	11	12	13	14	15
人数（人）	1	5	4	3	2	1