
 B .
B .  C .
C .  D .
D . 

下表是工作人员四次领取纸板数的记录:
|
日期 |
正方形纸板(张) |
长方形纸板(张) |
|
第一次 |
356 |
544 |
|
第二次 |
422 |
860 |
|
第三次 |
500 |
1000 |
|
第四次 |
988 |
2022 |
仓库管理员在核查时,发现一次记录有误.则记录有误的是第次.
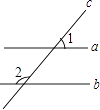
已知:如图, , CD平分
, EF平分
.
求证: .

证明:∵ ,
∴ ▲ ( ).
∵CD平分 , EF平分
,
∴∠1= ▲ , ∠2= ▲ .
∴∠ ▲ =∠ ▲ .
∴( ).
①若x满足 , 求
的值;
②若x满足 , 求
的值;

课本利用“三角形内角和是180°”和“对顶角相等”对此题进行了证明,小明同学提出了另外一种证明方法,如下思路框图:
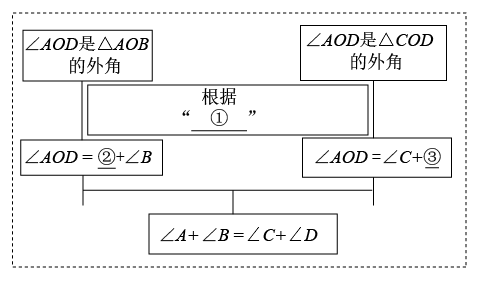
完成框图填空:①,②,③;
小慧同学把图1中线段AC与BD相交所组成的结构称为“8字形”,她对原题进行了改编:如图2,AC、BD相交于点O,∠BAC、∠BDC的角平分线交于点P, ,
, 求∠P的度数(用含
,
的式子表示).请你帮助小明完成以下问题:
小明看到图2中有两个与∠P相关的“8字形”,请你根据(1)的结论写出关于∠P的两个关系式为:①;②
;
小明进一步思考:设 ,
, 由
, 得
, ③
, 由①、③(或②、③)联立、转化、整理可得结论:
;
小慧同学为了寻找规律,再次改变条件:如图3,AC、BD相交于点O, ,
,
,
, 求
的度数(用含
,
的式子表示).请你写出解答: