河南省郑州枫杨外国语学校2022-2023学年九年级上学期开...

更新时间：2024-07-31 浏览次数：54 类型：开学考试

一、选择题(每题3分，共30分)

1. (2022九上·郑州开学考) 在学习《图形变化的简单应用》这一节时，老师要求同学们利用图形变化设计图案.下列设计的图案中，是中心对称图形不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022九上·郑州开学考) 下列性质中，正方形具有而矩形不一定具有的性质是（　　）

A . 对角线互相垂直 B . 对角线互相平分 C . 对角线相等 D . 四个角都是直角

答案解析收藏纠错 + 选题
3. (2022九上·郑州开学考) 把一个多边形割去一个角后，得到的多边形内角和为1440°，请问这个多边形原来的边数为（）

A . 9 B . 10 C . 11 D . 以上都有可能

答案解析收藏纠错 + 选题
4. (2022九上·郑州开学考) 为响应国家传统文化进校园的号召，某校准备购进一批毕加索笔来奖励经典诵读优秀生.某文具超市为让利给学校，经过两次降价，每支毕加索笔单价由121元降为100元，两次降价的百分率相同，设每次降价的百分率为x，根据题意列方程得（）

A . 121(1-x²)=100 B . 121(1+x)²=100 C . 121(1-2x)=100 D . 121(1-x)²=100

答案解析收藏纠错 + 选题
5. (2022九上·郑州开学考) 已知关于x的方程 $\text{[math]}$ = $\text{[math]}$ 的解是正整数，且k为整数，则k的值是（）

A . 0 B . -2 C . 0或6 D . -2或6

答案解析收藏纠错 + 选题
6. (2024九上·罗湖开学考) 如图，在平面直角坐标系中，若菱形ABCD的顶点A，B的坐标分别为(-3，0)，(2，0)，点D在y轴上，则点C的坐标是（）

A . (5，4) B . (4，5) C . (4，4) D . (5，3)

答案解析收藏纠错 + 选题
7. (2022九上·郑州开学考) 如图，已知∠BAC=60°，AD是角平分线且AD=10，作AD的垂直平分线交AC于点F，作DE⊥AC，则△DEF的长为（）

A . 10 B . 5+5 $\text{[math]}$ C . 5+5 $\text{[math]}$ D . 5 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九上·郑州开学考) 如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线折叠得到△AB'C， B'C交AD于点E，连接B'D，若∠B=60°，∠ACB=45°，AC=2 $\text{[math]}$ ，则B^，D的长是（）

A . 2 B . $\text{[math]}$ C . 2 $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·郑州开学考) 如图，A ， B为 $\text{[math]}$ 的正方形网格中的两个格点，称四个顶点都是格点的矩形为格点矩形，在此图中以A ， B为顶点的格点矩形共可以画出（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. (2022九上·郑州开学考) 如图，正方形ABCD的边长为10，E为AD的中点，连接CE，过点B作BF⊥CE交CD于点F，垂足为G，连接AG、DG，下列结论：
①BF=CE；②MG=CD；③∠CDG=∠AGE；④EG=2 $\text{[math]}$ ；⑤DG= $\text{[math]}$ CG.
其中在确结论有（）

A . ①②④ B . ②③⑤ C . ①②⑤ D . ①④⑤

答案解析收藏纠错 + 选题

二、填空题(每题3分，共15分)

11. (2022九上·郑州开学考) 对于非零的两个实数a，b，规定aUb=a³-ab，那么将aU16进行分解因式的结果为.

答案解析收藏纠错 + 选题
12. (2022九上·郑州开学考) 已知关于x的不等式组 $\text{[math]}$ 无实数解，则a的取值范围是.

答案解析收藏纠错 + 选题
13. (2022九上·郑州开学考) 已知△MBC∽△A^'B^'C^' ， AD和A^'D是对应的角平分线，若AD：AD'=4：3，△ABC的周长为16，则△AB'C的周长是.

答案解析收藏纠错 + 选题
14. (2022九上·郑州开学考) 如图在平行四边形ABCD中，E是CD的中点，F是AE的中点，CF交BE于点G，若BE=8，则GE=.

答案解析收藏纠错 + 选题
15. (2022九上·郑州开学考)
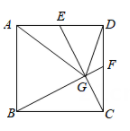
如图，矩形ABCD中，点P、Q分别是边AD和BC的中点，沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处，折痕交AB边于点E，交线段PQ于点G，若BC长为3，则线段FG的长为．

答案解析收藏纠错 + 选题

三、解答题(本大题共8个小题，共75分)

16. (2022九上·郑州开学考) 解方程：
1. （1） $\text{[math]}$ - $\text{[math]}$ =1
2. （2） x²-4x+1=0
答案解析收藏纠错 + 选题
17. (2022九上·郑州开学考) 先化简( $\text{[math]}$ -a-1)÷ $\text{[math]}$ ，然后从-1，0，1，3中选一个合适的数作为a的值代入求值.

答案解析收藏纠错 + 选题
18. (2022九上·郑州开学考) 如图，在网格中建立平面直角坐标系，每个小正方形边长都是1，其顶点叫做格点，△ABC的顶点都在格点上，A，B，C三点的坐标分别为(-1，0)，(0，3)，(-2，2).

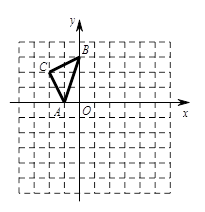
⑴将△ABC向右平移3个单位长度，得到△A₁B₁C₁ ，画出△A₁B₁C₁；

⑵以点O为对称中心，画出△A₁B₁C₁的中心对称图形△A₂B₂C₂；

⑶在（1）问的平移过程中，△ABC扫过的图形面积为 ▲ .

答案解析收藏纠错 + 选题
19. (2022九上·郑州开学考) 已知：关于x的一元二次方程x²-(2k+3)x+k²+3k+2=0.
1. （1）证明无论k取何值时方程总有两个实数根.
2. （2） △ABC中，BC=5，AB、AC的长是这个方程的两个实数根，求k为何值时，△ABC是等腰三角形？
答案解析收藏纠错 + 选题
20. (2022九上·郑州开学考) 已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH(即四边形ABCD的中点四边形).
1. （1）四边形EFGH的形状是 ▲ ，并证明你的结论.
2. （2）当AC、BD满足时，四边形EFGH是菱形.
3. （3）当AC、BD满足时，四边形EFGH是矩形.
4. （4）当AC、BD满足时，四边形EFGH是正方形.
答案解析收藏纠错 + 选题
21. (2022九上·郑州开学考) 某学校计划为“建党百年，铭记党史”演讲比赛购买奖品.已知购买3件A种奖品和2件B种奖品共需130元；购买5件A种奖品和4件B种奖品共需230元.
1. （1）求A，B两种奖品的单价各是多少元？
2. （2）学校准备购买A，B两种奖品共40件，A奖品的数量不少于B奖品数量的 $\text{[math]}$ ，且购买总费用不超过920元.当购买A种奖品多少件时，购买总费用最少？总费用最少是多少？
答案解析收藏纠错 + 选题
22. (2022九上·郑州开学考) 如图

【感知】如图①在△ABC中，点D为边BA延长线上的点，若 $\text{[math]}$ = $\text{[math]}$ ，过点D作DE∥BC交CA延长线于点E.若DE=5，求BC的长.

【探究】如图②，在△ABC中，点D是边AB上的点，点E为边AC的中点，连接BE、CD交于点F，若 $\text{[math]}$ = $\text{[math]}$ .小明尝试探究 $\text{[math]}$ 的值，在图②中.小明过点D作DM∥AC交BE于点M，易证△DFM∽△CFE，则 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ .从而得到 $\text{[math]}$ 的值为 ▲ ，易证△DBM∽△ABE，则 $\text{[math]}$ = $\text{[math]}$ ，从而得到 $\text{[math]}$ 的值为 ▲ ，从而得到 $\text{[math]}$ 的值为 ▲ .

【应用】如图③，在△ABC中，点D是边AB上的点，E为边CA延长线上的点，连接BE，延长CD，交BE于点F. $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ，且△ACD的面积为1，则△BDF的面积为 ▲ .

答案解析收藏纠错 + 选题
23. (2022九上·郑州开学考) 在平面直角坐标系xOy中，直线y=3x+6分别与x、y轴相交于A、B两点，将线段AB绕点A顺时针旋转90°得到线段AC．连接BC交x轴于点D.
1. （1）求点C的坐标；
2. （2） P为x轴上的动点，连接PB，PC，当|PB-PC|的值最大时，求此时点P的坐标．
3. （3）点E在直线AC上，点F在x轴上，若以B、D、E、F为顶点的四边形是平行四边形，请直接写出点F的坐标；
答案解析收藏纠错 + 选题