一、选择题(本大题共10小题,每小题4分,共40分)
-
-
A . 3x(x﹣4)=0
B . x2+y﹣3=0
C .  +x=2
D . x3﹣3x+8=0
+x=2
D . x3﹣3x+8=0
-
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 没有实数根
D . 无法确定
-
A . 1
B . ﹣1
C . ±1
D . 0
-
A . y轴
B . 直线x=2
C . 直线 D . 直线x=﹣3
D . 直线x=﹣3
-
A . (﹣2,2)
B . (2,﹣2)
C . (2,2)
D . (﹣2,﹣2)
-
A . 3或5
B . 5或6
C . 3或6
D . 3或5或6
-
8.
(2022九上·福州开学考)
已知二次函数y=(x+2)
2﹣1向左平移h个单位,再向下平移k个单位,得到二次函数y=(x+3)
2﹣4,则h和k的值分别为( )
A . 1,3
B . 3,﹣4
C . 1,﹣3
D . 3,﹣3
-
9.
(2022九上·福州开学考)
已知抛物线y=

(x﹣1)
2+k上有三点A(﹣2,y
1),B(﹣1,y
2),C(2,y
3),则y
1 , y
2 , y
3的大小关系为( )
A . y1>y2>y3
B . y3>y2>y1
C . y2>y3>y1
D . y2>y1>y3
-
10.
(2023九上·平定期中)
二次函数y=ax
2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
二、填空题(本大题共6小题,每小题4分,共24分)
-
-
-
-
14.
(2022九上·福州开学考)
某同学掷铅球,铅球的高y(m)与水平距离x(m)之间的函数关系式为y=﹣x
2+3x+18,则该同学的成绩是
m.
-
15.
(2022九上·福州开学考)
某小区中央花园有一块长方形花圃,它的宽为5m,若长边不变,将短边扩大,使得扩大后的花圃形状为正方形,且面积比原来增加15m
2 , 设原来花圃长边为xm,可列方程
.
-
三、解答题(本大愿共9题,共86分,解答应写出文字说明、证明过程或演算步骤.)
-
-
-
(2)

(y+2)
2﹣6=0.
-
18.
(2022九上·福州开学考)
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,﹣1),C(﹣3,2).

-
(1)
将△ABC绕点B顺时针旋转90°得到△A1B1C1 , 画出△A1B1C1;
-
-
19.
(2022九上·福州开学考)
若二次函数y=ax
2+bx﹣3的图象经过(﹣1,0)和(3,0)两点,求此二次函数的表达式,并指出其顶点坐标和对称轴.
-
-
(1)
如果此方程有两个不相等的实数根,求a的取值范围.
-
(2)
当a为何值时,方程的两个根互为倒数,求出此时方程的解.
-
21.
(2022九上·福州开学考)
研究所在研究某种流感病毒发现,若一人携带此病毒,未进行有效隔离,经过两轮传染后共有169人患病(假设每轮每人传染的人数相同),求:
-
-
(2)
如果这些病毒携带者,未进行有效隔离,按照这样的传染速度,第三轮传染后,共有多少人患病?
-
-
(1)
将抛物线的解析式化成y=a(x﹣h)2+k的形式(要求写出过程);
-
(2)
写出抛物线的对称轴和顶点坐标:当x取何值时,y随x的增大而减小;
-
(3)
若直线y=m与该抛物线有两个公共点,求m的取值范围.
-
23.
(2022九上·福州开学考)
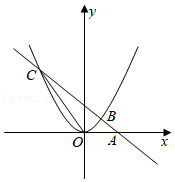
如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax
2交于B,C两点,点B坐标为(1,1).
-
-
-
(3)
当﹣x+2>ax2时,请观察图象直接写出x的取值范围.
-
24.
(2022九上·福州开学考)
如图,在足够大的空地上有一段长为a米的旧墙,农场决定利用旧墙和篱笆围成中间隔有一道篱笆的矩形菜园ABCD,其中AD≤a,已知矩形菜园的一边靠墙,共用了60米篱笆.

-
(1)
若a=20,所围成的矩形菜园的面积为225平方米,求所利用旧墙AD的长;
-
-
-
(1)
若函数y1的对称轴为直线x=2,且它的图象经过点(﹣a,b),求函数y1的解析式.
-
(2)
若函数y
2的图象经过点(r,0),其中r≠0,求证:函数y
1的图象经过点(

, 0).
-
(3)
设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
 B .
B . 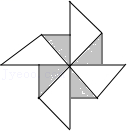 C .
C . 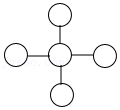 D .
D . 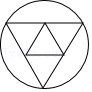
 B .
B .  C .
C .  D .
D . 



