山西省阳泉市盂县2021-2022学年八年级上学期期中数学试...

更新时间：2023-08-26 浏览次数：33 类型：期中考试

一、单选题

1. 以下是回收、绿色包装、节水、低碳四个标志，其中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019八上·瑞安期中) 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是（）

A . 1,2,1 B . 1,2,2 C . 1,2,3 D . 1,2,4

答案解析收藏纠错 + 选题
3. 下列图形中，对称轴条数最少的是（　　）

A . 正五边形 B . 正方形 C . 等边三角形 D . 圆

答案解析收藏纠错 + 选题
4. (2021八上·汨罗期中) 某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（）.

A . 带①去 B . 带②去 C . 带③去 D . ①②③都带

答案解析收藏纠错 + 选题
5. (2020八上·孝义期中) 如图，若 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019八上·孝义期中) 一个正多边形的一个外角是72°，则这个多边形是（）

A . 三角形 B . 五边形 C . 六边形 D . 七边形

答案解析收藏纠错 + 选题
7. (2017·邵阳模拟) 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（）

A . CB=CD B . ∠BAC=∠DAC C . ∠BCA=∠DCA D . ∠B=∠D=90°

答案解析收藏纠错 + 选题
8. (2018八上·常熟期末) 如图，在△ABC中，AC=AD=BD，∠B=35°，则∠CAD的度数为（）

A . 70° B . 55° C . 40° D . 35°

答案解析收藏纠错 + 选题
9. (2020八上·常熟月考) 如图，△ABC 中，AB=AC，AD 是∠BAC 的平分线，已知 AB=5，AD=3，则 BC的长为（）

A . 5 B . 4 C . 10 D . 8

答案解析收藏纠错 + 选题
10. (2018八上·天台期中) 如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·马龙月考)
如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是．

答案解析收藏纠错 + 选题
12. (2020八上·孝义期中) 如图，将一副三角板如图摆放，则图中 $\text{[math]}$ 的度数是度．

答案解析收藏纠错 + 选题
13. (2019八上·右玉期中) 如图△ABC中，∠B＝∠C，FD⊥BC，DE⊥AB，∠AFD＝158°，则∠EDF＝.

答案解析收藏纠错 + 选题
14. (2020八上·无锡月考) 如图是4×4正方形网络，其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有个.

答案解析收藏纠错 + 选题
15. (2020八上·孝义期中) 如图，将长方形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题

三、解答题

16. (2019八上·孝义期中) 已知：如图，点A，B，C，D在同一直线上，AE∥DF，BF∥EC，AB=CD．求证：AE=DF.

答案解析收藏纠错 + 选题
17. (2019八上·合肥月考) 如图，在△ABC中，AB＝AC ， AB的垂直平分线MN交AC于点D ，交AB于点E ．
1. （1）若∠A＝40°，求∠DBC的度数；
2. （2）若AE＝6，△CBD的周长为20，求△ABC的周长．
答案解析收藏纠错 + 选题
18. (2019八上·右玉期中) 如图，在平面直角坐标系中，A（3，4），B（1，2），C（5，1）．
1. （1）如图中作出△ABC关于y轴的对称图形△A₁B₁C₁；
2. （2）写出点A₁ ， B₁ ， C₁的坐标（直接写答案）．A₁：，B₁：，C₁：；
3. （3）求△ABC的面积．
答案解析收藏纠错 + 选题
19. 如图，Rt△ABC中，∠ACB＝90°，∠B＝50°，AD为∠BAC的平分线，F为AC上的点，DE⊥AB，垂足为E，DF＝DB．
1. （1）求证：DC＝DE；
2. （2）求证：△CDF≌△EDB；
答案解析收藏纠错 + 选题
20. 已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上一点．
1. （1）求证：BD=AE．
2. （2）判断AD与AE的位置关系，并说明理由．
答案解析收藏纠错 + 选题
21. (2019八上·孝义期中) 阅读下列材料，并完成任务．
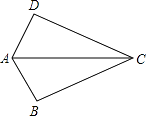
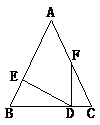
筝形的定义：两组邻边分别相等的四边形叫做筝形，几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说，如图，若四边形ABCD是一个筝形，则AB=AD，BC=CD；若AB=AD，BC=CD，则四边形ABCD是筝形.

如图，四边形ABCD是一个筝形，其中AB=AD，BC=CD．对角线AC，BD相交于点O，过点O作OM⊥AB，ON⊥AD，垂足分别为M，N.求证：四边形AMON是筝形.

答案解析收藏纠错 + 选题
22. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，线段 $\text{[math]}$ 经过点C，且 $\text{[math]}$ 于点D， $\text{[math]}$ 于点E．求证： $\text{[math]}$ ， $\text{[math]}$ ”这个问题时，只要证明 $\text{[math]}$ ，即可得到解决，
1. （1）积累经验：
  请写出证明过程；
2. （2）类比应用：
  如图2，在平面直角坐标系中， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点A的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ，求点B与x轴的距离．
3. （3）拓展提升：
  如图3， $\text{[math]}$ 在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ，点A的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ，求点B的坐标．
答案解析收藏纠错 + 选题
23. 综合与探究
[问题]如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点C作直线l平行于 $\text{[math]}$ ，点D在直线l上移动，角的一边DE始终经过点B，另一边 $\text{[math]}$ 与 $\text{[math]}$ 交于点P，研究 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系．
1. （1） [探究发现]
  如图2，某数学学习小组运用“从特殊到一般”的数学思想，发现当点D移动到使点P与点C重合时，很容易就可以得到 $\text{[math]}$ 请写出证明过程；
2. （2） [数学思考]
  如图3，若点P是 $\text{[math]}$ 上的任意一点(不含端点 $\text{[math]}$ )，受(1)的启发，另一个学习小组过点D， $\text{[math]}$ 交 $\text{[math]}$ 于点C，就可以证明 $\text{[math]}$ ，请完成证明过程；
3. （3） [拓展引申]
  若点P是 $\text{[math]}$ 延长线上的任意一点，在图(4)中补充完整图形，并判断结论是否仍然成立．
答案解析收藏纠错 + 选题