北京市通州区2021-2022学年八年级下学期期末数学试题

更新时间：2022-11-30 浏览次数：118 类型：期末考试

一、单选题

1. (2021·广元) 下列图形均表示医疗或救援的标识，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. 一元二次方程 $\text{[math]}$ 的二次项系数、一次项系数、常数项分别是（）

A . 1，3，-4 B . 0，3，4 C . 0，-3，4 D . 1，-3，-4

答案解析收藏纠错 + 选题
3. 在下列条件中，能判定四边形为矩形的是（）

A . 两组对边分别平行 B . 四个内角度数相等 C . 对角线长度相等 D . 对角线互相垂直

答案解析收藏纠错 + 选题
4. (2022九上·雁塔月考) 如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的值是（）

A . 0 B . 2 C . 0，2 D . 0，-2

答案解析收藏纠错 + 选题
5. (2021八下·房山期末) 某少年军校准备从甲、乙、丙三位同学中选拔一人参加全市射击比赛．在选拔比赛中，三个人10次射击成绩的统计结果如下表．
同学
最高水平/环
平均数/环
中位数/环
方差
甲
10
8.3
8.5
1.5
乙
10
8.3
8.5
2.8
丙
10
8.3
8.5
3.2
经比较，推荐甲参加比赛，理由是甲的（）

A . 最高水平较高 B . 平均水平较高 C . 成绩好的次数较多 D . 射击技术稳定

答案解析收藏纠错 + 选题
6. 在某游乐场，以中心广场为观测点，若有序数对 $\text{[math]}$ 表示图中“太阳神车”的位置，有序数对 $\text{[math]}$ 表示图中“雪域金翅”的位置，则与图中“天地双雄”位置对应的有序数对为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 对频数分布直方图的下列认识，错误的是（）

A . 每小组条形图的横宽等于这组的组距 B . 每小组条形图的纵高等于这组的频数 C . 每小组条形图的面积等于这组的频率 D . 所有小组条形图的个数等于数据分组整理的组数

答案解析收藏纠错 + 选题
8. (2021八下·朝阳期末) 如图，中国国家博物馆收藏了元代制作的计时工具“铜壶滴漏”，这是目前发现形制最大、最完备的一个多级滴漏，从1316年使用到1919年，一直为人民报时、计时．从上至下的四个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”，通过多级滴漏，使得“星壶”中的水可以匀速滴入圆柱形的“受水壶”中，“受水壶”中带有刻度的木箭随着水位匀速上移，对准标尺就能读出相应的时间．在一天中，“受水壶”中的水面高度h与时间t的函数图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. 一个多边形的内角和是720°，那么这个多边形是边形．

答案解析收藏纠错 + 选题
10. 在平面直角坐标系 $\text{[math]}$ 中有一点 $\text{[math]}$ ，请你写出一个一次函数表达式，使得这个一次函数的图象经过点 $\text{[math]}$ ．这个表达式为：．

答案解析收藏纠错 + 选题
11. (2020·丰南模拟) 关于x的方程的 $\text{[math]}$ 有两个相等的实数根，则m的值为．

答案解析收藏纠错 + 选题
12. 若 $\text{[math]}$ ， $\text{[math]}$ 是一次函数 $\text{[math]}$ 的图象上的两个点，则 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是 $\text{[math]}$ $\text{[math]}$ （“>”，“=”或“<”）．

答案解析收藏纠错 + 选题
13. 在菱形ABCD中，两条对角线AC＝8，BD＝6，则此菱形的高为．

答案解析收藏纠错 + 选题
14. 某注册平台三月份新注册用户为653万，五月份新注册用户为823万，设四、五两个月新注册用户每月平均增长率为 $\text{[math]}$ ，则列出的方程是．

答案解析收藏纠错 + 选题
15. 寒假期间，滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试，每次测试成绩分别为5分，4分，3分，2分，1分五档，甲、乙两位同学在这个项目的测试成绩统计结果如图所示：
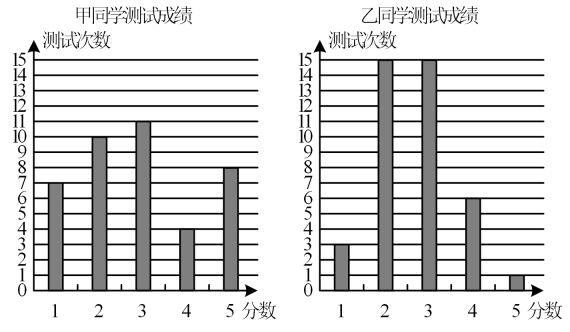
结合图中数据，请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩．

答案解析收藏纠错 + 选题
16. 如图五边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．将它放入某平面直角坐标系后，若顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题

三、解答题

17. (2019九上·河源月考) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2022八下·湖里期末) 如图，在▱ABCD中，E，F分别在AD，BC上，且AE=CF，连结BE、DF．求证：BE=DF．

答案解析收藏纠错 + 选题
19. (2020九上·海淀期中) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根．
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）若 $\text{[math]}$ 为正整数，求此时方程的根．
答案解析收藏纠错 + 选题
20. (2021八下·通州期末) 已知一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与正比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ．
（ $\text{[math]}$ ）分别求 $\text{[math]}$ ， $\text{[math]}$ 的值；

答案解析收藏纠错 + 选题
21. 已知：线段 $\text{[math]}$ ，以线段 $\text{[math]}$ 为对角线，求作：矩形 $\text{[math]}$ ．
小明的作法如下．
作法：
①分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于： $\text{[math]}$ 的同样长为半径作弧，两弧分别交于点 $\text{[math]}$ ， $\text{[math]}$ ；
②作直线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ；③以点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 长为半径作圆；④作圆 $\text{[math]}$ 的直径 $\text{[math]}$ （异于直径 $\text{[math]}$ ）；⑤连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所以四边形 $\text{[math]}$ 即为所求作的知形．
1. （1）请你用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明．.
  证明：∵ $\text{[math]}$ ， $\text{[math]}$
  ∴ $\text{[math]}$ 是线段 $\text{[math]}$ 的垂直平分线（）
  ∴点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点．
  ∴ $\text{[math]}$ ，又∵ $\text{[math]}$ ， ∴ $\text{[math]}$
  ∴四边形 $\text{[math]}$ 是矩形（）（填推理的依据）．
答案解析收藏纠错 + 选题
22. 用长为6米的铅合金条制成如图所示的矩形窗框，其中 $\text{[math]}$ // $\text{[math]}$ // $\text{[math]}$ ，设窗框的高度为 $\text{[math]}$ 米．
1. （1）设窗框宽度 $\text{[math]}$ 为 $\text{[math]}$ 米，则 $\text{[math]}$ 米（用含 $\text{[math]}$ 的代数式表示）；
2. （2）当窗户的透光面积为1.5平方米时，请你计算出窗框的高和宽分别是多少米（铝合金条的宽度忽略不计）
答案解析收藏纠错 + 选题
23. 只有一组对边平行的四边形叫做梯形，平行的两条边叫做梯形的底，不平行的两条边叫做梯形的腰；两腰相等的梯形叫做等腰梯形，如图，四边形 $\text{[math]}$ 是等腰梯形，请你结合我们学习四边形的经验，猜想并证明等腰梯形的一条性质．
1. （1）文字描述性质；
2. （2）证明过程
  已知： ▲
  求证： ▲
  证明：
答案解析收藏纠错 + 选题
24. 秋季新学期开学时，某中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：
分数段
频数
频率
$\text{[math]}$
9
$\text{[math]}$
$\text{[math]}$
36
0.4
$\text{[math]}$
27
0.3
$\text{[math]}$
$\text{[math]}$
0.2
请根据上述统计图表，解答下列问题：
1. （1）在表中， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）补全频数分布直方图；
3. （3）根据以上的数据，如果90分以上（含90分）算做优秀，该学校有七年级学生1000名，请你估算一下该学校七年级学生成绩优秀的人数．
答案解析收藏纠错 + 选题
25. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 中点.过点 $\text{[math]}$ 作 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）请你直接写出当 $\text{[math]}$ 满足什么条件时，四边形 $\text{[math]}$ 为菱形．
答案解析收藏纠错 + 选题
26. 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与 $\text{[math]}$ 的交点为点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；
2. （2）已知点 $\text{[math]}$ ，经过 $\text{[math]}$ 作平行于 $\text{[math]}$ 轴的直线，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，过 $\text{[math]}$ 点作平行于 $\text{[math]}$ 轴的直线，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 时，判断线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；
  ②若 $\text{[math]}$ ，结合函数的图象，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. 已知点 $\text{[math]}$ ， $\text{[math]}$ 分别是正方形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 上的动点，并且保持 $\text{[math]}$ ，请你证明 $\text{[math]}$ 的周长是一个只与正方形 $\text{[math]}$ 边长有关的定值．

答案解析收藏纠错 + 选题