山西省晋城市阳城县2021-2022学年八年级上学期期末数学...

更新时间：2022-11-08 浏览次数：38 类型：期末考试

一、单选题

1. (2023七下·仙居期末) 下列各数中，是无理数的是（）

A . $\text{[math]}$ B . 0 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·潘集模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八上·阳城期末) 下列说法正确的是（）

A . $\text{[math]}$ 是无理数 B . 7的平方根是 $\text{[math]}$ C . 实数 $\text{[math]}$ 介于6和7之间 D . 0.000000022可以用科学记数法表示为 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·钦州期末) 等腰三角形的一个内角为70°，则另外两个内角的度数分别是（）

A . 55°，55° B . 70°，40°或70°，55° C . 70°，40° D . 55°，55°或70°，40°

答案解析收藏纠错 + 选题
5. (2021八上·阳城期末) 下列命题的逆命题是真命题的是（）

A . 如果 $\text{[math]}$ ，那么， $\text{[math]}$ B . 如果一个三角形有一个角是钝角，那么它的另外两个角是锐角 C . 角平分线上的点到角两边的距离相等 D . 如果一个整数的个位数字是5，那么这个整数能被5整除

答案解析收藏纠错 + 选题
6. (2024七下·江油月考) 课后延时服务已经落地，为了进一步对课后延时服务进行规范，某校计划在延时服务时间内开展各种社团活动．小明对全校学生进行抽样调查，收集整理拟参加社团活动类型（A．读书交流，B．体育锻炼，C．戏剧说唱，D．手工陶艺）数据后，绘制出两幅不完整的统计图，则下列说法错误的是（）

A . 样本容量为400 B . 类型D所对应的扇形的圆心角为36° C . 类型C所占的百分比为 $\text{[math]}$ D . 类型B的人数为120人

答案解析收藏纠错 + 选题
7. (2021八上·阳城期末) 公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 $\text{[math]}$ ，导致了第一次数学危机． $\text{[math]}$ 是无理数的证明如下：
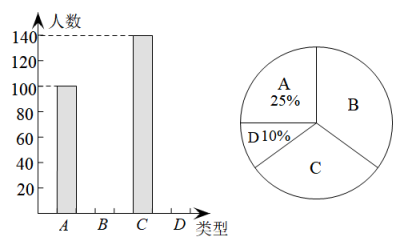
假设 $\text{[math]}$ 是有理数，那么它可以表示成 $\text{[math]}$ （p与q是互质的两个正整数）．于是 $\text{[math]}$ ，所以， $\text{[math]}$ ．于是 $\text{[math]}$ 是偶数，进而q是偶数．从而可设 $\text{[math]}$ ，所以 $\text{[math]}$ ， $\text{[math]}$ ，于是可得p也是偶数．这与“p与q是互质的两个正整数”矛盾，从而可知“ $\text{[math]}$ 是有理数”的假设不成立，所以 $\text{[math]}$ 是无理数．
这种证明“ $\text{[math]}$ 是无理数”的方法是（）

A . 综合法 B . 反证法 C . 举反例法 D . 数学归纳法

答案解析收藏纠错 + 选题
8. (2023·东方模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，适当长为半径画弧，分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，再分别以点 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 为半径画弧，两弧交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交边 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021八上·阳城期末) 七巧板是我们祖先的一项创造，它来源于勾股法，被誉为“东方魔板”，如图所示是一副七巧板，若已知等腰直角三角形 $\text{[math]}$ 的面积是1，则正方形的 $\text{[math]}$ 边长是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2022八下·高阳期末) 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）

A . 1，4，5 B . 2，3，5 C . 3，4，5 D . 2，2，4

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·临淄月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2021八上·阳城期末) 若 $\text{[math]}$ ，直接写出 $\text{[math]}$ ； $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023九上·桂平期中) 要表示一个家庭一年用于“教育”， “服装”，“食品”，“其他”这四项的支出各占家庭本年总支出的百分比，从“扇形统计图”，“条形统计图”，“折线统计图”中选择一种统计图，最适合的统计图是.

答案解析收藏纠错 + 选题
14. (2021八上·阳城期末) 如图是一个重要公式的几何解释，请你写出这个公式．

答案解析收藏纠错 + 选题
15. (2021八上·阳城期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ 边的垂直平分线交 $\text{[math]}$ 于点D，交 $\text{[math]}$ 于点E，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的周长是．

答案解析收藏纠错 + 选题
16. (2021八上·阳城期末) 为推动“双减”政策落实，切实解决学生负担，严格控制作业时间．政教处拟对全校560名学生每天做作业所用时间进行调查，调查人员随机抽取了部分学生进行问卷调查，并把结果制成如图所示的统计图，根据统计图可以估计这所学校学生“双减”政策落实后，每天做作业时间不少于1小时的人数为．

答案解析收藏纠错 + 选题
17. (2021八上·阳城期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线，E是边 $\text{[math]}$ 上一点，过点C作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点F，当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
18. (2021八上·阳城期末) 如图，在边长为6的正方形 $\text{[math]}$ 内作 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021八上·阳城期末)
1. （1）计算： $\text{[math]}$
2. （2）先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2021八上·阳城期末)
1. （1）计算： $\text{[math]}$ ．
2. （2）计算： $\text{[math]}$
3. （3）因式分解： $\text{[math]}$
4. （4）因式分解： $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2021八上·阳城期末) 一辆装满快递的物流卡车，其外形为高2.5米，宽1.6米的箱式货车，要开进厂门形状如图所示的工厂，问这辆车能否通过该工厂的厂门（厂门上方为半圆形拱门）？

答案解析收藏纠错 + 选题
22. (2021八上·阳城期末) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点A，C，D依次在同一直线上，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）连接 $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ ，时，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2021八上·阳城期末) 为落实“双减”和“五项管理”，促进每一个孩子全面发展、健康成长，各级各部门都做出了有力举措．某班同学分三组进行教学实践活动调查，三组同学分别对七年级40名同学作业管理情况，八年级30名同学读物管理情况，九年级30名同学睡眠管理情况进行全面调查，并分别用扇形图、频数分布直方图、表格来描述得到的数据．
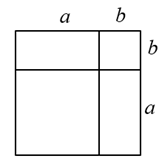
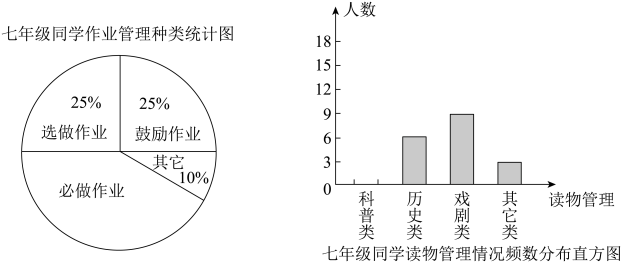
九年级同学睡眠管理时间情况统计表
时间
9小时左右
10小时左右
11小时左右
8小时左右
人数（人）
5
8
12
5
根据以上信息，请回答下列问题：
1. （1）七年级40名同学中必做作业的人数是多少？
2. （2）补全八年级30名同学读物管理情况频数分布直方图：
3. （3）九年级30名同学睡眠时间的平均时间大约是多少小时？
答案解析收藏纠错 + 选题
24. (2021八上·阳城期末) 已知 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，（给出条件：① $\text{[math]}$ ， ② $\text{[math]}$ ．在这2个条件中选择一个补充在前面的横线上），则 $\text{[math]}$ 的长是否存在？若存在，求出 $\text{[math]}$ 的长；若不存在，请说明理由．

答案解析收藏纠错 + 选题
25. (2021八上·阳城期末) 问题情境：已知，如下图，在梯形 $\text{[math]}$ 中， $\text{[math]}$ 直线l， $\text{[math]}$ 直线l，垂足分别为D，E，点C在直线l上， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）猜想证明：
  如图①，试判断 $\text{[math]}$ 的形状，并说明理由；
2. （2）解决问题：
  如图①，若 $\text{[math]}$ ，求梯形 $\text{[math]}$ 的面积；
3. （3）拓展提升：
  如图②，设梯形 $\text{[math]}$ 的周长为m， $\text{[math]}$ 边中点O处有两个动点P，Q同时出发，沿着 $\text{[math]}$ 的方向移动，点Q的速度是点P速度的3倍，当点P第一次到达点B时，两点同时停止移动．
  ①两点同时停止移动时，点Q移动的路程与点P移动的路程之差 $\text{[math]}$ ．（填“>”“<”或“=”）
  ②移动过程中点P能否和点Q相遇？如果能，则用直线a连接相遇点和点O，并探索直线a与 $\text{[math]}$ 的位置关系，写出推理过程：如不能，说明理由．
答案解析收藏纠错 + 选题