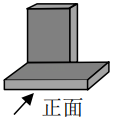
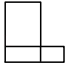
 B .
B . 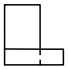 C .
C . 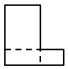 D .
D . 










①则m的值为;
②若A2022在反比例函数y=(x>0)的图象上,对应点B2022在“位似反比例函数”y=
(x<0)的图象上,求证:BB2022=2AA2022;

①如图1,若点O是BC的中点,AD=6,BC=8,则AD2=,BC2=,(AB+CD)2=;
②如图2,AO:DO=1:3,AO=3,BO=4,则AD2=,BC2=,(AB+CD)2=;
请利用图2证明你发现的关系式;
如图3,在矩形ABCD中,E,F两点均在AD边上,BE⊥CF交于G点,EF:BE=1:4,CF=3,BC=4.求证:CG=CD;
如图4,已知BD为△ABC的中线,CE⊥BD交AB于点E,交BD于点F,AE=5,BD=10,EC=15,求BC的长.