内蒙古自治区赤峰市松山区2021-2022学年八年级上学期期...

更新时间：2022-12-13 浏览次数：78 类型：期末考试

一、单选题

1. (2022八上·松山期末) 下列图形不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023七下·西安月考) 化简： $\text{[math]}$ 的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八上·柳州期末) 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如，利用图1可以得到 $\text{[math]}$ ，那么利用图2所得到的数学等式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022八上·松山期末) 2020年12月17日嫦娥五号返回器携带月球样品安全着陆，标志着中国航天事业向前又迈出了一大步．嫦娥五号返回器在接近大气层时，飞行1m大约需要0.0000893s．数0.0000893用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八上·松山期末) 一个多边形的每一个外角都等于40°，那么这个多边形的内角和为（）

A . 1260° B . 1080° C . 1620° D . 360°

答案解析收藏纠错 + 选题
6. (2022八上·松山期末) 点 $\text{[math]}$ （－1，2）关于 $\text{[math]}$ 轴对称的点的坐标为（）

A . （1，2） B . （1，－2） C . （－1，2） D . （－1，－2）

答案解析收藏纠错 + 选题
7. (2022八上·松山期末) 若分式 $\text{[math]}$ 的值为零，则x的值为（）

A . 2或－2 B . 2 C . －2 D . 1

答案解析收藏纠错 + 选题
8. (2022八上·松山期末) 下列命题：①等腰三角形的角平分线、中线和高三线重合；②等腰三角形底边的中点到两腰的距离相等；③等腰三角形一定是锐角三角形；④等腰三角形两个底角相等；⑤等腰三角形是轴对称图形．其中真命题的个数是（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
9. (2023七下·青岛期末) 如图，为了测量池塘两岸相对的A，B两点之间的距离，小明同学在池塘外取AB的垂线BF上两点C，D，BC=CD，再画出BF的垂线DE，使点E与A，C在同一条直线上，可得△ABC≌△EDC，从而DE=AB．判定△ABC≌△EDC的依据是（）

A . ASA B . SAS C . AAS D . SSS

答案解析收藏纠错 + 选题
10. (2022八上·松山期末) 定义 $\text{[math]}$ ，例如 $\text{[math]}$ ，则 $\text{[math]}$ 的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2022八上·松山期末) 如图，在△ABC中，AD、CE是中线，若四边形BDFE的面积是6，则△ABC的面积为（）

A . 12 B . 15 C . 18 D . 24

答案解析收藏纠错 + 选题
12. (2022八上·松山期末) 用正三角形和正六边形铺成一个平面，则在同一个顶点处，正三角形和正六边形的个数之比为（）

A . 4:1 B . 1:1 C . 1:4 D . 4:1或1:1

答案解析收藏纠错 + 选题
13. (2022八上·松山期末) 如图，在正方形ABCD中，点E，F分别在BC，CD上，AE＝AF，AC与EF相交于点G．下列结论：①AC垂直平分EF；②BE＋DF＝EF；③当∠DAF＝15°时，△AEF为等边三角形；④当∠EAF＝60°时，∠AEB＝∠AFD．其中正确的结论是（）

A . ①③ B . ②④ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
14. (2022八上·松山期末) 已知： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ …，若 $\text{[math]}$ 符合前面式子的规律，则 $\text{[math]}$ 的值是（）

A . 90 B . 89 C . 100 D . 109

答案解析收藏纠错 + 选题

二、填空题

15. (2022八上·松山期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022八上·松山期末) 如图，△ABC是等边三角形，E是AC上一点，D是BC延长线上一点，连接BE和DE，如果∠ABE＝40°，BE＝DE．则∠CED＝°．

答案解析收藏纠错 + 选题
17. (2022八上·松山期末) 如图，为使人字梯更为巩固，在梯子中间安装一个横向“拉杆”，所根据的数学原理是．

答案解析收藏纠错 + 选题
18. (2022八上·松山期末)
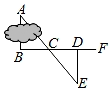
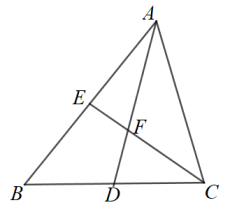
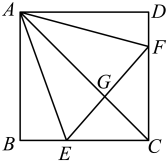
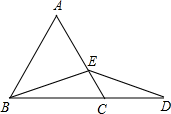
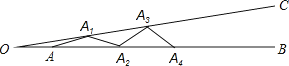
如图，∠BOC=9°，点A在OB上，且OA=1，按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A₁ ，得第1条线段AA₁；再以A₁为圆心，1为半径向右画弧交OB于点A₂ ，得第2条线段A₁A₂；再以A₂为圆心，1为半径向右画弧交OC于点A₃ ，得第3条线段A₂A₃；…这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n= ．

答案解析收藏纠错 + 选题

三、解答题

19. (2023七下·全椒期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2022八上·松山期末)
1. （1）先化简： $\text{[math]}$ ，再选择你最喜欢的a的值代入式子中，求出代数式的值．
2. （2）计算： $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2022八上·松山期末) 小明同学过生日，爸爸给他买了一块如图所示的三角形蛋糕，如果∠C＝90°，∠B＝30°；切蛋糕时，爸爸让小明想办法把蛋糕切成大小、形状完全一样的三份．你能帮助小明解决这个问题吗？
1. （1）把你的思路用尺规作图画出来，保留必要的作图痕迹．
2. （2）把你的方法用推理的方式加以说明．
答案解析收藏纠错 + 选题
22. (2022八上·松山期末) 一位沙漠吉普爱好者驾车从甲站到乙站与大部队汇合，出发2小时后车子出了点故障，修车用去半小时时间，为了弥补耽搁的时间，他将车速增加到原来的1.6倍，结果按时到达，已知甲、乙两站相距100千米，求他原来的行驶速度．

答案解析收藏纠错 + 选题
23. (2022八上·松山期末) 如图，△ABC是边长为4的等边三角形，点P在AB上，过点P作PE⊥AC，垂足为E，延长BC到点Q，使CQ＝PA，连接PQ交AC于点D，求DE的长．

答案解析收藏纠错 + 选题
24. (2022八上·松山期末) 问题背景：某课外学习小组在一次学习研讨中，得到如下命题题设，请分别补充结论，不用证明．
1. （1）如图1，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM与CN有何大小关系？
2. （2）如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM与CN有何大小关系？
3. （3）学习小组成员根据上述两个命题运用类比的思想又提出了如下的问题：如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM与CN的大小关系是怎样的？请说明理由．
4. （4）请你继续完成下面的探索：
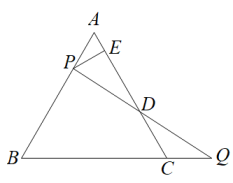
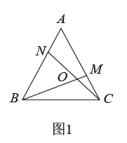
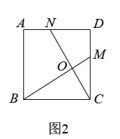
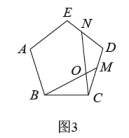
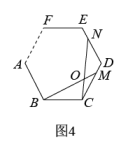
  如图4，在正n边形（n≥3）中，M、N分别是CD、DE上的点，BM与CN相交于点O，问当∠BON等于多少度时，结论BM＝CN成立？（不要求证明）
答案解析收藏纠错 + 选题
25. (2022八上·松山期末) 小郝同学在当建造师的爸爸的一份资料上看到一段文字：“民用住宅窗户面积应小于地板面积，但窗户面积与地板面积的比值越大，住宅的采光条件会越好．”
小郝思考：如果同时增加相等的窗户面积和地板面积，住宅的采光条件会不会更好？为了验证这猜想，小郝做了如下数学实验：
第一步：假设某住宅窗户面积为17平方米，地板面积为80平方米，则 $\text{[math]}$ ．如果窗户面积和地板面积同时增加1平方米，则 $\text{[math]}$ ，此时：
∵ $\text{[math]}$ ，
∴ $\text{[math]}$ ，
所以，同时增加相等的窗户面积和地板面积，住宅的采光条件会更好．
第二步：假设某住宅窗户面积为x平方米，地板面积为y平方米，且y>x>0，则 $\text{[math]}$ ，如果窗户面积和地板面积同时增加1平方米，则 $\text{[math]}$ ．
请帮小郝完成猜想证明过程．
第三步：假设某住宅窗户面积为x平方米，地板面积为y平方米，且y>x>0，则 $\text{[math]}$ ．如果窗户面积和地板面积同时增加m平方米，则 $\text{[math]}$ ．
请帮小郝完成猜想证明过程，井对问题下结论．

答案解析收藏纠错 + 选题
26. (2022八上·松原期末) 如图，在平面直角坐标系中，点O为坐标原点，等腰直角三角形OAB的斜边OB在x轴上，∠OAB＝90°，点A（3，3）．
1. （1）求点B的坐标；
2. （2）点P从点O出发沿x轴以每秒2个单位的速度向x轴正方向运动，设点P运动时间为t秒，求t为何值时，OP＝2PB；
3. （3）在（2）的条件下，当OP＝2PB时，在第一象限内是否存在点Q，使△BPQ为等腰直角三角形？若存在，请直接写出点Q的坐标；（写出四个即可）若不存在，请说明理由．
答案解析收藏纠错 + 选题