广西壮族自治区南宁市广西大学附属中学2021-2022学年九...

更新时间：2022-11-30 浏览次数：66 类型：期中考试

一、单选题

1. (2023九上·五华期中) 数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021九上·南宁期中) $\text{[math]}$ 的半径为 $\text{[math]}$ ，点 $\text{[math]}$ 到圆心 $\text{[math]}$ 的距离为 $\text{[math]}$ ，点 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是（）

A . 点 $\text{[math]}$ 在 $\text{[math]}$ 内 B . 点 $\text{[math]}$ 在 $\text{[math]}$ 上 C . 点 $\text{[math]}$ 在 $\text{[math]}$ 外 D . 无法确定

答案解析收藏纠错 + 选题
3. (2023九上·惠阳期中) 下列说法中，正确的是（）

A . 掷一枚质地均匀的硬币，正面朝上是必然事件 B . 打开电视机，正在播放广告这一事件是随机事件 C . 明天会下雨是不可能事件 D . “彩票中奖的概率为 $\text{[math]}$ ”表示买 $\text{[math]}$ 张彩票一定有 $\text{[math]}$ 张会中奖

答案解析收藏纠错 + 选题
4. (2021九上·南宁期中) 在平面直角坐标系中，将二次函数 $\text{[math]}$ 的图像向左平移2个单位，再向下平移2个单位，平移后的解析式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九上·南宁期中) 如图是一个可以自由转动的转盘，转盘分成4个大小相同的扇形，颜色分为灰、白二种颜色．指针的位置固定，转动的转盘停止后，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形），则指针指向白色区域的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
6. (2021九上·南宁期中) 如图， $\text{[math]}$ 圆O的直径，弦 $\text{[math]}$ ，垂足为M，下列结论不成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021九上·南宁期中) 某品牌网上专卖店1月份的营业额为50万元，已知第一季度的总营业额共218万元，如果平均每月增长率为x，则由题意列方程应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·南宁期中) 若关于x的一元二次方程x²+4x+m＝0有两个不相等的实数根，则m的取值范围是（）

A . m＞﹣4 B . m＞4 C . m≤﹣4 D . m＜4

答案解析收藏纠错 + 选题
9. (2021九上·南宁期中) 我国古代数学著作《九章算术》有题如下：“今有邑方二百步，各中开门.出东门一十五步有木.问出南门几何步而见木？”大意是，今有正方形小城 $\text{[math]}$ 的边长 $\text{[math]}$ 为200步，如图，各边中点分别开一城门，走出东门E15步处有树Q.问出南门F多少步能见到树Q（即求从点F到点P的距离）？（注：步是古代的计量单位）（）

A . $\text{[math]}$ 步 B . $\text{[math]}$ 步 C . $\text{[math]}$ D . $\text{[math]}$ 步

答案解析收藏纠错 + 选题
10. (2021九上·南宁期中) 如图，以正方形 $\text{[math]}$ 的 $\text{[math]}$ 边为直径作半圆O过点C作直线切半圆于点F，交 $\text{[math]}$ 边于点E，若 $\text{[math]}$ 的周长为12，则线段 $\text{[math]}$ 的长为（）

A . 1 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021九上·南宁期中) 一次函数 $\text{[math]}$ 与二次函数 $\text{[math]}$ 在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
12. (2021九上·南宁期中) 如图，在平面直角坐标系中，点A的坐标为（ $\text{[math]}$ ， 0），点C的坐标为（0，6），将矩形OABC绕O按顺时针方向旋转α度得到OA′B′C′，此时直线 $\text{[math]}$ 、直线 $\text{[math]}$ 分别与直线 $\text{[math]}$ 相交于点P、Q.当 $\text{[math]}$ ，且 $\text{[math]}$ 时，线段 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2023九上·城厢开学考) 在平面直角坐标系中，点P（﹣3，1）关于坐标原点中心对称的点P′的坐标是.

答案解析收藏纠错 + 选题
14. (2021九上·南宁期中) 如图，AB为⊙O的直径，C ， D两点在圆上，∠CAB＝20°，则∠ADC的度数等于

答案解析收藏纠错 + 选题
15. (2021九上·南宁期中) 如图，圆锥的底面半径OB为5cm，它的侧面展开图扇形的半径AB为15cm，则这个扇形的圆心角的度数为．

答案解析收藏纠错 + 选题
16. (2021九上·南宁期中) 已知 a、b 是方程 x²﹣2x﹣1＝0 的两个根，则 a²﹣a+b 的值是．

答案解析收藏纠错 + 选题
17. (2021九上·南宁期中) 如图：正方形DGFE的边EF在△ABC边BC上，顶点D、G分别在边AB、AC上，AH⊥BC于H，交DG于P，已知BC＝48，AH＝16，那么S_正方形DGEF＝.

答案解析收藏纠错 + 选题
18. (2021九上·南宁期中) 设O为坐标原点，点A、B为抛物线 $\text{[math]}$ 上的两个动点，且 $\text{[math]}$ .连接点A、B，过O作 $\text{[math]}$ 于点C，则点C到y轴距离的最大值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021九上·南宁期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2022九上·大安月考) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2021九上·南宁期中) 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中， $\text{[math]}$ 的三个顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均在格点上.
1. （1）画出 $\text{[math]}$ 向左平移5个单位后的图形 $\text{[math]}$ ，并写出 $\text{[math]}$ 点的坐标.
2. （2）画出 $\text{[math]}$ 绕 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 后的图形 $\text{[math]}$ ，并写出 $\text{[math]}$ 点的坐标.
3. （3）在（2）的条件下，求 $\text{[math]}$ 到 $\text{[math]}$ 所经过的路径长.
答案解析收藏纠错 + 选题
22. (2021九上·南宁期中) “垃圾分类，从我做起”，为改善群众生活环境，提升全民文明素养，垃圾分类已经在武威市普及开来.垃圾一般可分为可回收垃圾（A），厨余垃圾（B），有害垃圾（C），其它垃圾（D）四类.市民甲拿了一袋有害垃圾，乙拿了一袋厨余垃圾，随机扔进并排的4个垃圾桶A，B，C，D.
1. （1）甲扔对垃圾的概率为；
2. （2）用列表法或树状图求出甲、乙两人同时扔对垃圾的概率.
答案解析收藏纠错 + 选题
23. (2021九上·南宁期中) 如图，正三角形、正方形、正六边形等正n边形与圆的形状有差异，我们将正n边形与圆的接近程度称为“接近度”.
1. （1）角的“接近度”定义：设正n边形的每个内角的度数为 $\text{[math]}$ ，将正n边形的“接近度”定义为 $\text{[math]}$ .于是 $\text{[math]}$ 越小，该正n边形就越接近于圆，
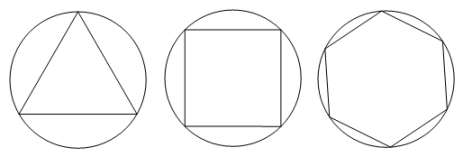
  ①若 $\text{[math]}$ ，则该正n边形的“接近度”等于.
  ②若 $\text{[math]}$ ，则该正n边形的“接近度”等于.
  ③当“接近度”等于.时，正n边形就成了圆.
2. （2）边的“接近度”定义：设一个正n边形的外接圆的半径为R，正n边形的中心到各边的距离为d，将正n边形的“接近度”定义为 $\text{[math]}$ .分别计算 $\text{[math]}$ 时边的“接近度”，并猜测当边的“接近度”等于多少时，正n边形就成了圆？
答案解析收藏纠错 + 选题
24. (2021九上·南宁期中) 某服装批发市场销售一种衬衫，衬衫每件进货价为50元.规定每件售价不低于进货价，经市场调查，每月的销售量y（件）与每件的售价x（元）满足一次函数关系，部分数据如下表：

售价x（元/件）

60

65

70

销售量y（件）

1400

1300

1200
1. （1）求出y与x之间的函数表达式；（不需要求自变量x的取值范围）
2. （2）该批发市场每月想从这种衬衫销售中获利24000元，又想尽量给客户实惠，该如何给这种衬衫定价？
3. （3）物价部门规定，该衬衫的每件利润不允许高于进货价的50%，设销售这种衬衫每月的总利润为w（元），求w与x之间的函数关系式，x为多少时，w有最大值，最大利润是多少？
答案解析收藏纠错 + 选题
25. (2021九上·南宁期中) 如图，以 $\text{[math]}$ 的直角边 $\text{[math]}$ 为直径作⊙O，交斜边 $\text{[math]}$ 于点A， $\text{[math]}$ 于点D，点F是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 与 $\text{[math]}$ 相交于点G，延长 $\text{[math]}$ 与 $\text{[math]}$ 的延长线相交于点P.
1. （1）求证： $\text{[math]}$ 是⊙O的切线；
2. （2）求证：点G为 $\text{[math]}$ 的中点；
3. （3）若 $\text{[math]}$ ，且⊙O的半径长为3，求 $\text{[math]}$ 的长度.
答案解析收藏纠错 + 选题
26. (2021九上·南宁期中) 如图1，在平面直角坐标系xOy中，抛物线y＝-x²+bx+c交x轴于A，B两点（A在B左侧），交y轴于点C，且OC＝OB＝3，对称轴l交抛线于点D，交x轴于点G.
1. （1）求抛物线的表达式及顶点坐标；
2. （2）如图2，过点C作CH⊥DG于H，在射线HG上有一动点M（不与H重合），连接MC，将MC绕M点顺时针旋转90°得线段MN，连接DN，在点M的运动过程中， $\text{[math]}$ 是否为定值？若是，求出该定值；若不是，说明理由；
3. （3）如图3，将抛物线y＝-x²+bx+c向右平移后交直线l于点E，交原抛物线于点Q且点Q在第一象限，过点Q作QP⊥x轴于点P，设点Q的横坐标为m，问：在原抛物线y＝-x²+bx+c上是否存在点F，使得以P，Q，E，F为顶点的四边形是平行四边形？若存在，求出m的值；若不存在，说明理由.
答案解析收藏纠错 + 选题