| x | 0 | 0.5 | 1 | 1.5 | 2 |
| y=ax2+bx+c | ﹣1 | ﹣0.5 | 1 | 3.5 | 7 |
| x | …… | 0 | | 4 | …… |
| y | …… | 0.32 | ﹣2 | 0.32 | …… |

… | -2 | -1 | 0 | 1 | 2 | … | |
… | 0 | 4 | 6 | 6 | 4 | … |
则下列说法中正确的个数是( )
①方程有两根为
,
;②抛物线与y轴的交点为
;③抛物线的对称轴是直线
;④抛物线开口向上;
①b>0;②a﹣b+c=0;③当x<﹣1或x>3时,y>0;④一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根.
上述结论中正确的是.(填上所有正确结论的序号)
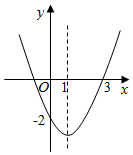
| x | -1 | - | 0 | | 1 | | 2 | | 3 |
| y | -2 | | 1 | | 2 | | 1 | | -2 |
一元二次方程 (a≠0,a,b,c是常数)的两个根
的取值范围是下列选项中的哪一个 (填序号)
① ②
③ ④
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … | |
y | … | 3 | m | ﹣1 | 0 | ﹣1 | 0 | 3 | … |
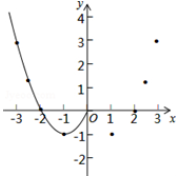
①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是.



解:画出函数y=x2﹣2x﹣2的图象,它与x轴的公共点的横坐标大约是﹣0.7,2.7.所以方程x2﹣2x﹣2=0的实数根为x1≈﹣0.7,x2≈2.7.我们还可以通过不断缩小根所在的范围估计一元二次方程的根.……这种求根的近似值的方法也适用于更高次的一元方程.

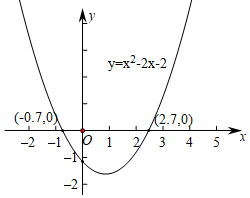
根据你对上面教材内容的阅读与理解,解决下列问题:
①请在网格内画出函数y=|x2﹣4x+3|的图象;
②若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解,求m的取值范围;
③若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解x1 , x2 , x3 , x4(x1<x2<x3<x4),满足x4﹣x3=x3﹣x2=x2﹣x1 , 求m的值.