2023年浙教版数学八年级下册第三章数据分析初步单元测试...

更新时间：2023-01-22 浏览次数：133 类型：单元试卷

一、单选题（每题3分，共30分）

1. (2021八下·绍兴期中) 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A . 20 B . 18 C . 15 D . 14

答案解析收藏纠错 + 选题
2. (2023·唐山模拟) 若一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数为4，方差为3，那么数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数和方差分别是（）

A . 4， 3 B . 6 $\text{[math]}$ 3 C . 3 $\text{[math]}$ 4 D . 6 5

答案解析收藏纠错 + 选题
3. (2024八下·凉州期末) 颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩（以“次”为单位计）为：52，50，46，54，50，56，47，52，53，50．则以下数据中计算错误的是（）

A . 平均数为51 B . 方差为8.4 C . 中位数为53 D . 众数为50

答案解析收藏纠错 + 选题

4. (2022八下·鲅鱼圈期末) 下列表格反映了某公司员工的工资情况，该公司的应聘者最应该关注的数据是（）

职位	普工	文员	经理	董事长
人数	8	6	2	1
工资/元	2200	2600	4000	12000

A . 平均数 B . 众数与中位数 C . 方差 D . 最大数据

答案解析收藏纠错 + 选题

5. (2020八下·余干期末) 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A . 平均数和中位数不变 B . 平均数增加，中位数不变 C . 平均数不变，中位数增加 D . 平均数和中位数都增大

答案解析收藏纠错 + 选题
6. (2022八下·斗门期末) 甲组数据为4、5、6、7；乙组数据为3、5、6、8，下列说法正确的是（）

A . 甲更稳定 B . 乙更稳定 C . 方差一样 D . 无法比较

答案解析收藏纠错 + 选题
7. (2022八下·成都期末) 将数据a、b、e、d、e、f的每一个数据都增加5，则下列说法中错误的是（）

A . 平均数增加5 B . 中位数增加5 C . 众数增加5 D . 方差增加5

答案解析收藏纠错 + 选题
8. (2022八下·高安期末) 一组数据： $\text{[math]}$ 的平均数为 $\text{[math]}$ ，众数为 $\text{[math]}$ ，中位数为 $\text{[math]}$ ，则以下判断正确的是（）

A . $\text{[math]}$ 一定出现在 $\text{[math]}$ 中 B . $\text{[math]}$ 一定出现在 $\text{[math]}$ 中 C . $\text{[math]}$ 一定出现在 $\text{[math]}$ 中 D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都不会出现在 $\text{[math]}$ 中

答案解析收藏纠错 + 选题
9. (2022八下·南昌期末) 从一组数据中取出a个x₁ ， b个x₂ ， c个x₃ ，组成一个样本，那么这个样本的平均数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021八下·兴隆期末)
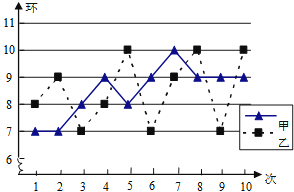
在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①S_甲²＞S_乙²；②S_甲²＜S_乙²；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定，由统计图可知正确的结论是（　　）

A . ①③ B . ①④ C . ②③ D . ②④

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. 已知一组数据23，25，20，15，x，15，若它们的中位数是21，那么它们的平均数为。

答案解析收藏纠错 + 选题
12. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

答案解析收藏纠错 + 选题
13. (2021八下·鄞州期中) 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S² ，那么数据a+99，b+100，c+101的方差将 S²（填“大于”“小于”或“等于”）.

答案解析收藏纠错 + 选题
14. 某学校九（1）班40名同学的期中测试成绩分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，……， $\text{[math]}$ .已知 $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +……+ $\text{[math]}$ = 4800，y= $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +……+ $\text{[math]}$ ，当y取最小值时，的值为.

答案解析收藏纠错 + 选题
15. (2022八下·新余期末) 已知一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数是3，则数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数是．

答案解析收藏纠错 + 选题
16. (2022八下·西城期末) 射击运动员小东10次射击的成绩（单位：环）：7.5，8，7.5，8.5，9，7，7，10，8.5，8．这10次成绩的平均数是8.1，方差是0.79，如果小东再射击一次，成绩为10环，则小东这11次成绩的方差0.79．（填“大于”、“等于”或“小于”）

答案解析收藏纠错 + 选题

三、解答题（共9题，共72分）

17. 已知一组数据：x，10，12，6的中位数与平均数相等，求x的值。

答案解析收藏纠错 + 选题
18. 已知5个数a₁ ， a₂ ， a₃ ， a₄ ， a₅的平均数为m，则
1. （1） a₁ ， a₂ ， a₃ ， 0，a₄ ， a₅ ，这6个数的平均数为；
2. （2） 2a₁ ， 2a₂ ， 2a₃ ， 2a_4，2a₅这5个数的平均数为；
3. （3）若5个数b₁ ， b₂ ， b₃ ， b₄ ， b₅的平均数为n，则2a₁+b₁ ， 2a₂+b₂ ， 2a₃+b₃ ， 2a₄+b₄ ， 2a₅+b₅这5个数的平均数为。
答案解析收藏纠错 + 选题
19. 某排球队6名场上队员的身高（单位：cm）是180，184，188，190，192，194.现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员身高的方差会变化吗？通过计算说明你的理由。

答案解析收藏纠错 + 选题
20. (2022八下·怀仁期末) 6月的第三个星期天是父亲节，某校组织了以“父爱如山”为主题的演讲比赛，根据初赛成绩，七、八年级各选出 $\text{[math]}$ 名学生组成代表队，参加决赛．并根据他们的决赛成绩绘制了如下两幅统计图表：(满分为 $\text{[math]}$ 分)
1. （1）补全下表中的数据；
  组别
  平均数(分)
  中位数(分)
  众数(分)
  七年级
  $\text{[math]}$
  八年级
  $\text{[math]}$
  $\text{[math]}$
2. （2）结合两队决赛成绩的平均数和中位数，评价两个队的决赛成绩；
3. （3）哪个年级代表队的决赛成绩更稳定．
答案解析收藏纠错 + 选题
21. (2020八下·海沧期末) 端午假期刚过，集美龙舟队有开始新的一轮训练，为更加有效训练队员，集美龙舟队决定公开招聘教练，经过笔试后筛选出甲、乙两位教练进行面试和体侧，两人的成绩如右表．
1. （1）当体侧成绩权重为6，面试成绩权重为4，请问甲、乙两人谁的成绩高？
2. （2）当体侧成绩权重为 $\text{[math]}$ ，面试和体侧各有权重，并且权总和为10，请问当 $\text{[math]}$ 取什么范围，乙成绩比甲高？
答案解析收藏纠错 + 选题
22. (2023八下·晋城期末) 山西某中学王老师为了选拔一名优秀的学生参加市内的数学比赛，对两名备赛选手进行了6次测验，两位同学的测验成绩如表所示：
（参考公式 $\text{[math]}$ ）

第1次
第2次
第3次
第4次
第5次
第6次
平均成绩
中位数
众数
方差
甲
83
85
90
80
85
87
85
a
85
b
乙
86
86
83
84
85
86
c
85.5
d
$\text{[math]}$
根据表中提供的数据，解答下列问题：
1. （1） a的值为，d的值为．
2. （2）求b和c的值，并直接指出哪位同学的成绩更稳定．
3. （3）根据以上信息，你认为王老师应该选哪位同学参加比赛，请说明理由．
答案解析收藏纠错 + 选题
23. (2022八下·新余期末) 每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共1200名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：
七年级抽取的学生的竞赛成绩：
4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．
根据以上信息，解答下列问题：
1. （1）填空：a=，b=，c=；
2. （2）根据以上数据分析，从中位数来看，年级成绩更优异；从合格率来看，年级成绩更优异；从方差来看，年级成绩更整齐；
3. （3）估计该校七、八年级共1200名学生中竞赛成绩达到9分及以上的约有多少人？
答案解析收藏纠错 + 选题
24. (2022八下·滨城期末) 为迎接建党一百周年，学校组织了六次党史知识测试，甲、乙两名同学部分成绩如图所示，已知甲、乙两名同学六次成绩的平均数相等．
1. （1）计算甲同学成绩的平均数，直接写出乙同学第六次成绩；
2. （2）甲同学成绩的中位数和众数分别为和，乙同学成绩的中位数和众数分别为和；
3. （3）若乙同学成绩的方差为 $\text{[math]}$ ，请计算甲同学成绩的方差，并比较哪个同学的成绩较稳定？
答案解析收藏纠错 + 选题
25. (2022八下·盘龙期末) 《生物多样性公约》第十五次缔约方大会（COP15）重新确定于2021年5月17日至30日在云南省昆明市举办．“生物多样性”的目标、方法和全球通力合作，将成为国际范围的热点关注内容．为广泛宣传云南生物多样性，某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试．现分别在七、八两个年级中各随机抽取了10名学生，统计这部分学生的竞赛成绩，相关数据统计、整理如下：
【收集数据】
七年级10名同学测试成绩统计如下：
72，84，72，91，79，69，78，85，75，95
八年级10名同学测试成绩统计如下：
85，72，92，84，80，74，75，80，76，82
【整理数据】两组数据各分数段，如下表所示：
成绩
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
七年级
1
5
2
a
八年级
0
4
5
1
【分析数据】两组数据的平均数、中位数、众数、方差如下表：
年级
统计量
平均数
中位数
众数
方差
七年级
80
b
72
66.6
八年级
80
80
c
$\text{[math]}$
【问题解决】根据以上信息，解答下列问题：
1. （1）填空：a=，b=，c=；
2. （2）计算八年级同学测试成绩的方差是： $\text{[math]}$ $\text{[math]}$ ．请估计哪个年级的竞赛成绩更整齐？
3. （3）按照比赛规定90分及其以上算优秀，请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人？
4. （4）根据以上数据，你认为该校七、八年级中哪个年级学生知识竞赛成绩更好？请说明理由（至少写出两条理由）．
答案解析收藏纠错 + 选题