
已知:如图1, .

求作:等边 , 使得等边
内接于
.
作法:
①如图2,作半径;
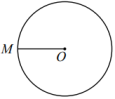
②以M为圆心,长为半径作弧,交
于点A,B,连接
;
③以B为圆心,长为半径作弧,交
于点C;
④连接 ,
.
∴就是所求作的等边三角形.
根据上述尺规作图的过程,回答以下问题:
证明:连接 ,
,
,
.
由作图可知 ,
∴ ,
是等边三角形.
∴ ▲
.
∴ .
∵ ,
∴ . ( )(填推理的依据)
∵ ,
∴是等边三角形.
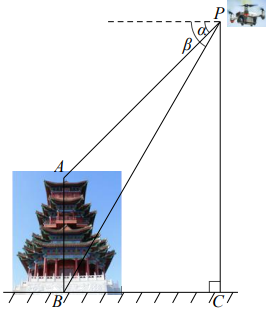
水平距离x/m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
垂直高度y/m | 0.7 | 1.6 | 2.3 | 2.8 | 3.1 | 3.2 | 3.1 | … |

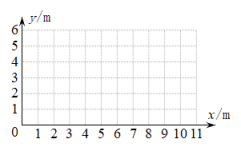
请根据测得的数据,解决以下问题:
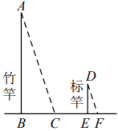
①依题意补全图1,猜想与
之间的数量关系,并证明;
②用等式表示线段 ,
的数量关系,并证明.