一、选择题(每小题只有一个选项符合题意,请将所选选项填涂在答题卡上,本大题共10个小题,每小题3分,共30分)
-
-
2.
(2023八上·岳池期末)
熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播经测量, 医用外科口罩的熔喷布厚度约为0.000 156米.将数据0.000 156用科学记数法表示应为( )
A . 0.156×10-3
B . 1.56×10-3
C . 1.56×10-4
D . 15.6×10-4
-
3.
(2023八上·岳池期末)
用一根小木棒与两根长分别为3cm和6cm的小木棒首尾顺次相连组成三角形,则这根小木棒的长度可以为( )
A . 3cm
B . 4cm
C . 9cm
D . 10 cm
-
A . (x2)3=x5
B . (-3x3y)2=9x9y2
C . x6÷x2=x3
D . -x2·x=-x3
-
-
A . 15
B . 11
C . 7
D . 3
-
7.
(2023八上·岳池期末)
如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为( )

A . 1
B .  C . 2
D .
C . 2
D . 
-
-
9.
(2023八上·岳池期末)
如图,在等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件中的一个,不能判定△ABE≌△ACD的是( )

A . AD=AE
B . ∠DCB=∠EBC
C . ∠ADC=∠AEB
D . BE=CD
-
10.
(2023八上·岳池期末)
若关于x的一元一次不等式组

的解集是x≤a,且关于y的分式方程

有非负整数解,则符合条件的所有整数a的和为( )
A . 6
B . 4
C . 1
D . 0
二、填空题(请把最简答案填写在答题卡相应的位置.本大题共6个小题,每小题3分,共18分)
-
-
-
-
-
15.
(2023八上·岳池期末)
如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E.若S
△ABC=7,DE=2,AB=4,则AC的长是

-
16.
(2023八上·岳池期末)
如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF与AD相交于点G,与BE相交于点H.在下面给出的四个结论中,正确的是
(填序号)
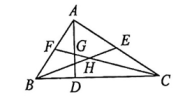
①△ABE的面积等于△BCE的面积
②∠AFG=∠AGF
③∠FAG=2∠ACF
④BH=CH.
三、解答题(本大题共4个小题,第17小题5分,第18~20小题各6分,共23分)
-
-
-
-
20.
(2023八上·岳池期末)
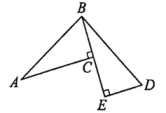
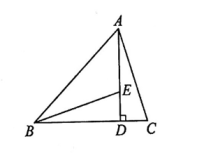
如图,已知AD是△ABC的边BC上的高,E为AD上一点,且BE=AC,DE=DC.
求证:∠DBE=∠DAC.
四、实践应用题(本大题共4个小题,第21 小题6分,第22~24小题各8分,共30分)
-
21.
(2023八上·岳池期末)
如图,在正方形网格中建立平面直角坐标系xOy中,已知△ABC的三个顶点都在格点(网格小正方形的顶点)上,点A的坐标为(4,4).

( 1 )画出△ABC关于y轴对称的图形△A1B1C1 , 并写出点A的对应点A1的坐标;
( 2 )在x轴上求作一点P,使PB + PC的值最小. (不写作法,保留作图痕迹)
-
-
(1)
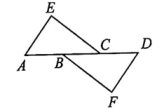
若∠B=35°,∠E=25°,求∠CAE的度数;
-
-
23.
(2023八上·岳池期末)
某快递仓库原来是人工分拣货物,为提高工作效率,现使用机器人分拣货物.已知一台机器人的工作效率相当于一名工人工作效率的20倍,且用一台机器人分拣6000件货物,比原来30名工人分拣这些货物多用

小时.
-
-
(2)
此仓库元旦前夕收到货物68万件,为了在6小时内分拣完所有货物,公司调配了20台机器人和20名工人,工作3小时后,又调配了15台机器人进行增授,该公司能否在规定的时间内完成任务?请说明理由.
-
24.
(2023八上·岳池期末)
如图,在△ABC中,AB=AC,∠B=50°,D是边BC上的一个动点(点D不与点B,C重合),连接AD,作∠ADE=50°,DE与AC相交于点E.

-
(1)
当BD=CE时,求证:△ABD≌△DCE ;
-
(2)
当△ADE是等腰三角形时,求∠BAD的度数.
五、推理论证题
-
25.
(2023八上·岳池期末)
已知x≠1.观察下列等式:
(1-x)(1+x)=1-x2
;
(1-x)(1+x+x2)=1-x3;
(1-x)(1+x+x2+x3)=1-x4;
-
(1)
猜想: (1-x)(1+x+x2+x3+……+xn-1)=;
-
-
(3)
根据你的猜想计算:(x-1)(x2023+x2022+x2021+……+x2+x+1).
六、拓展探究题
-
-
(1)
问题发现:
如图1,△ABC和△EDC都是等边三角形,点B,D,E在同一条直线上,连接AE,则∠AEC的度数为,线段AE,BD之间的数量关系为;
-
(2)
拓展探究:
如图2,△ABC和△EDC都是等腰直角三角形,且∠ACB=∠DCE=90°,点B,D,E在同一条直线上,CM为△EDC中DE边上的高,连接AE,试求∠AEB的度数及线段CM,AE,BM之间的数量关系,并说明理由;
-
(3)
解决问题:
如图3,△ABC和△EDC都是等腰三角形,∠ACB=∠DCE=36°,点B,D,E在同一条直线上,请直接写出∠EAB+∠ECB的度数.
 B .
B .  C .
C .  D .
D .