
月份 | 1 | 2 | 3 | 4 | 5 |
接种人数(万人) | 1.2 | 1.8 | 1.6 | 2.1 | 1.8 |


名称 | A | B |
批发价(元/ | 4 | 3 |
零售价(元/ | 6 | 4 |
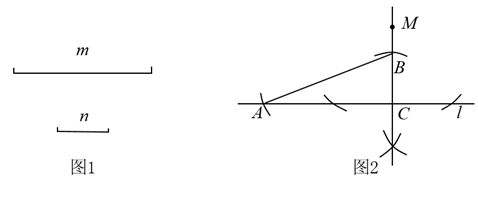
数学课上,老师出示了如下题目:如图1,已知线段m,n.运用尺规作图画出 , 使斜边
, 一条直角边
.


将调查结果绘制成如下所示的条形统计图和扇形统计图(均不完整)

请根据统计图中提供的信息,解答下列问题:
“飞天梦永不失重,科学梦张力无限”的主题活动,包含了以下四个内容:A.书写观后感;B.演示科学实验;C.绘制手抄报;D.开展主题班会.王老师在四张完全相同的卡片上分别写了A,B,C,D,然后背面朝上放置,搅匀后要求先由七年级派一名代表从中随机抽取一张,记下标号后放回,再由八年级派一名代表从中随机抽取一张,请用列表或画树状图的方法,求两个年级代表抽到的主题卡片中有演示科学实验(B)的概率.



勾股定理,是指直角三角形的两条直角边的平方和等于斜边的平方.在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派.
中国古代称直角三角形为勾股形(直角边中较小者为勾,另一长直角边为股,斜边为弦),周朝时期的商高提出了“勾三股四弦五”的特例,所以我国称这个定理为勾股定理,也有人称商高定理.
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。下面是小明搜集到的勾股定理的一种证明方法(不完整).
如图,在中,
,
,
,
.
求证: .
证明:作出的外接圆O.延长
到点D,使得
. 连接
, 交
于点E.延长
与
的延长线交于点M.连接
, 延长
与
交于点N
∵ , ∴
,
为
的直径.
∴ . (依据1)
∴ ,
…

学习任务:
数学活动课上,老师让同学们根据下面情境提出问题并解答.
问题情境:在中,点P是边
上一点.将
沿直线
折叠,点D的对应点为E.
“兴趣小组”提出的问题是:如图1,若点P与点A重合,过点E作 , 与
交于点F,连接
, 则四边形
是菱形.

请你帮助他们解决此问题.