
 B .
B .  C .
C .  D .
D . 
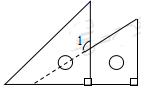
甲:如图 , 在
上找点E,连接
, 使
, 作
, 交
于F点,完成分割;
乙:如图 , 在
上找点F,连接
, 使
, 以
为直径作圆,交
于点E,连接
即可完成分割.下列结论正确的是( )



里程/公里 | 收费/元 |
3公里以下(含3公里) | 14 |
3公里以上,10公里以下(含10公里),每增加1公里 |
|
10公里以上,每增加1公里 |
当时,收费y(元)与行驶里程x(公里)的函数关系式为.
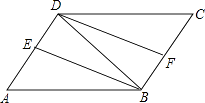


第一步:求平均数的公式是;
第二步:在该问题中,n=4, ,
,
,
;
第三步: .
①小宇的分析是错误的,他错在第几步?
请你帮他计算出正确的平均数,并估计这360名学生共植树多少棵.

项目 | 购进数量(件) | 购进所需费用(元) | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 7560 |
第二次 | 40 | 30 | 5880 |