①最小的“可拆分”整数是5;
②一个“可拆分”整数的拆分方式可以不只有一种;
③最大的“不可拆分”的两位整数是96.
其中正确的个数是( )
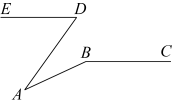
如图, , 当
与
满足什么关系时,
?
小明认为时
, 他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:
解:用直尺和圆规,在的右侧找一点M,使
(只保留作图痕迹).
∵ ,
∴① ▲
∵
∴② ▲
,
∵ ,
∴③ ▲
,
∴④ ▲
∴.
所以满足的关系为:当时,
.
甲试验基地抽取的20株树苗的长度:28,29,32,34,38,40,42,45,46,51,51,52,54,55,55,55,55,57,60,61.
乙试验基地抽出的20株树苗中,A、B、E三个等级的数据个数相同,C组的所有数据是:42,43,46,49,49.
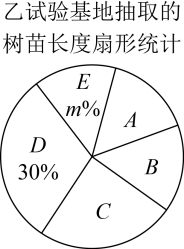
甲、乙两试验基地抽取的树苗长度的统计表
品种 | 平均数 | 中位数 | 众数 | E组所占百分比 |
甲 | 47 | 51 | a | |
乙 | 47 | b | 56 |
根据以上信息,解答下列问题:
例如: ,
∵ ,
∴1514是“和差数”.
又如: ,
∵ ,
∴2526不是“和差数”.
①求点的坐标;
②若点在反比例函数
的图象上,点
在
轴上,以点
为顶点的四边形能否为平行四边形?若能,直接写出点
的坐标;若不能,请说明理由.
①旋转至如图②,用等式表示
与
的数量关系,并证明你的结论;
②旋转至如图③,在①的结论下,
的延长线交
于点H,E为
的中点,且
, 直接写出
的长 ▲ .