
| 成绩/分 | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则这些学生决赛成绩的众数是( )
 B .
B .  C .
C .  D .
D . 


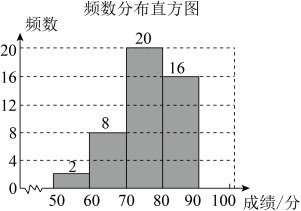
分组 | 频数 |
2 | |
8 | |
20 | |
16 | |
a | |
合计 | 50 |
频数分布表
|
用求差法比较大小 学习了不等式的知识后,我们根据等式和不等式的基本性质,可知比较两个数或式子的大小可以通过求它们的差来判断.如果两个数或式子为m和n,那么 当 当 当 反过来也符合题意,即 当 当 当 因此,我们经常把要比较的对象先数量化,再求它们的差,根据差的正负判断对象的大小.这种比较大小的方法被称为“求差法”. 例如:已知 解: ∵ ∴ ∴ ∴ “求差法”的实质是把两个数(或式子)的大小判断的问题,转化为一个数(或式子)与0的大小比较的问题.一般步骤为①作差;②变形;③判断符号;④得出结论. |
请解决以下问题:
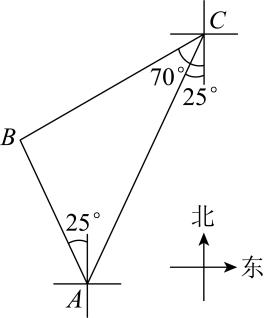
已知在中,
,
, 四边形
是正方形,H为
所在的直线与
的交点;如图,当点F在
上时,请判断
和
的关系,并说明理由.

如图,将正方形绕点C旋转,当点D在直线
右侧时,求证:
;
将正方形绕点C旋转一周,当
时,若
,
, 请直接写出线段
的长.