 C .
C . 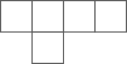 D .
D . 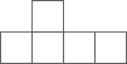
| 株数(株) | 7 | 9 | 12 | 2 |
| 花径(cm) | 6.5 | 6.6 | 6.7 | 6.8 |
这批“金心大红”花径的众数为( )
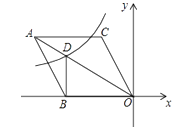

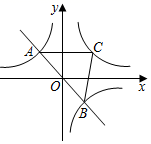
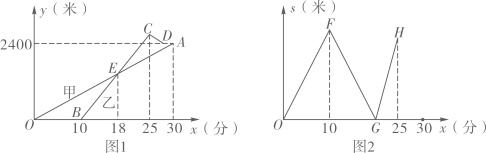
根据图1和图2中所给信息,解答下列问题:
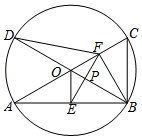
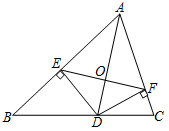
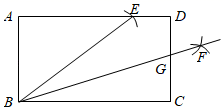
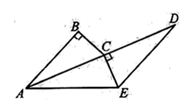
①求证:PE=PF.
②若DF=EF,求∠BAC的度数.
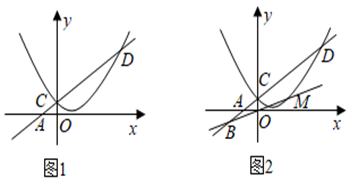
①N为x轴上一点,当四边形CDMN为平行四边形时,求点M的坐标;
②如图2,点M在直线CD下方,直线OM(OM∥CD的情况除外)交直线CD于点B , 作直线BD关于直线OM对称的直线B ,当直线B
与坐标轴平行时,直接写出点M的横坐标.